| Mart – Nisan – Mayıs | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | |||||
Olaylar
- 491 – Flavius Anastasius, Bizans İmparatoru oldu.
- 1899 – İspanya, Puerto Rico’yu ABD’ye bıraktı.
- 1905 – Einstein, görelilik kuramını açıkladı.
Özel görelilik

Fizikte, özel görelilik teorisi (kısaca özel görelilik) veya izafiyet teorisi, uzay ve zaman arasındaki ilişkiyi açıklayan bir bilimsel teoridir.[1] Albert Einstein’ın orijinal çalışmalarında teori, iki varsayıma dayanmaktadır:[2][3]
- Fizik yasaları, tüm süredurum referans çerçevelerinde (yani ivmesiz referans çerçevelerinde) değişmezdir (yani aynıdır).
- Işık kaynağının veya gözlemcinin hareketinden bağımsız olarak vakumdaki ışığın hızı, tüm gözlemciler için aynıdır.
1905’te Albert Einstein tarafından Annalen der Physik dergisinde, “Hareketli cisimlerin elektrodinamiği üzerine” isimli makalenin ikinci sayfasında açıklanan ve ardından beşinci sayfasındaki “bir cismin atıllığı enerji içeriği ile bağlantılı olabilir mi?” başlıklı makaleyle pekiştirilmesiyle ortaya çıkmıştır. Teoriye göre bütün varlıklar ve varlığın fiziksel olayları görelidir. Zaman, mekan, hareket, birbirlerinden bağımsız değildirler. Aksine bunların hepsi birbirine bağlı, göreli olaylardır. Nesne zamanla, zaman nesneyle, mekan hareketle, hareket mekanla ve dolayısıyla hepsi birbiriyle bağımlıdır. Bunlardan hiçbiri bağımsız değildir, kendisi bu konuda şöyle demektedir:
Zaman ancak hareketle, cisim hareketle, hareket cisimle vardır. O halde; cisim, hareket ve zamandan birinin diğerine bir önceliği yoktur. Galilei’nin Görelilik Prensibi, zamanla değişmeyen hareketin göreceli olduğunu; mutlak ve tam olarak tanımlanmış bir hareketsiz halinin olamayacağını önermekteydi. Galileo’nin ortaya attığı fikre göre; dış gözlemci tarafından hareket ettiği söylenen bir gemi üzerindeki bir kimse geminin hareketsiz olduğunu söyleyebilir.
Einstein’ın teorisi, Galilei’nin Görelilik Prensibi ile doğrusal ve değişmeyen hareketinin durumu ne olursa olsun tüm gözlemcilerin ışığın hızını her zaman aynı büyüklükte ölçeceği önermesini birleştirir. Bu teori sezgisel olarak algılanamayacak, ancak deneysel olarak kanıtlanmış birçok ilginç sonuca varmamızı sağlar. Özel görelilik teorisi, uzaklığın ve zamanın gözlemciye bağlı olarak değişebileceğini ifade ederek Newton’ın mutlak uzay zaman kavramını anlamsızlaştırır. Uzay ve zaman gözlemciye bağlı olarak farklı algılanabilir. Bu teori, madde ile enerjinin ünlü E=mc² formülü ile birbirine bağlı olduğunu da gösterir (c ışık hızıdır). Özel Görelilik teorisi, tüm hızların ışık hızına oranla çok küçük olduğu uygulama alanlarında Newton mekaniği ile yaklaşık aynı sonuçları verir.
Teorinin özel ifadesiyle anılmasının nedeni, görelilik ilkesinin yalnızca eylemsiz gözlem çerçevesine uygulanış şekli olmasından kaynaklanır. Einstein, tüm gözlem çerçevelerine uygulanan ve yerçekimi kuvvetinin etkisinin de hesaba katıldığı Genel Görelilik teorisini geliştirmiştir. Özel Görelilik, yerçekimi kuvvetini hesaba katmaz ancak ivmeli gözlemcilerin durumunu da inceler. Özel Görelilik, günlük yaşamımızda mutlak olarak algıladığımız, zaman gibi kavramların göreli olduğunu söylemesinin yanı sıra, sezgisel olarak göreceli olduğunu düşündüğümüz kavramların ise mutlak olduğunu ifade eder. Birbirlerine göre hareketi nasıl olursa olsun tüm gözlemciler için ışığın hızının aynı olduğunu söyler. Özel Görelilik, c katsayısının sadece belli bir doğa olayının –ışık– hızı olmasının çok ötesinde, uzay ile zamanın birbiriyle ilişkisinin temel özelliği olduğunu ortaya çıkarmıştır. Özel Görelilik ayrıca, hiçbir maddenin ışığın hızına ulaşacak şekilde hızlandırılamayacağını söyler.
Öngörüleri
Özel görelilik, kendi zamanı için inanılması güç, pek çok öngörülerde bulunmuştur. Bunlardan en önemlileri:
- Nesneler hızlandıkça zaman nesne için daha yavaş akmaya başlayacaktır, ışık hızına ulaşıldığında zaman durmalıdır.
- Nesneler hızlandıkça kütlelerinin bir kısmı kinetik enerjiye dönüşür, durağan kütleye sahip cisimler hiçbir zaman ışık hızına erişemeyeceklerdir.
- Cisimler hızlandıkça hareket doğrultusundaki boyları kısalmaya uğrayacaktır.
- Hiçbir cisim ışık hızında veya daha hızlı gidemez.
Özel görelilik, mantığımıza ve sağ duyumuza aykırı bir evren tanımladığından, bilim insanları 100 yılı aşkın bir süredir bunun doğruluğunu gözleri ile görmek ve bir açık bulmak umudu ile deneyler yapıp durmaktadırlar. Bu öngörülerin pek çoğu 1905’ten günümüze dek defalarca denenmiş ve doğru çıkmıştır:
- İçlerinde çok hassas atom saatleri taşıyan uçaklar değişik yönlere doğru değişik hızlarla hareket ettirilmiş ve saatlerin kuramın hesaplarına yeterince uygun olarak yavaşladığı/hızlandığı gözlenmiştir.[4]
- Zamandaki yavaşlamanın sadece saatte meydana gelmediğini, gerçekte yaşandığının kanıtı ilk olarak nötrino ve mü-mezon deneylerinde ortaya çıkmıştır. Güneşten dünyaya gelen nötrino ve müonların ışık hızına çok yaklaştıkları (%99,5) için ömürlerinin (yaşam sürelerinin) Dünya’da üretilen durağan olanlara göre çok daha uzun olduğu görülmektedir.[5]
- Parçacık hızlandırıcılarındaki hızlandırma deneylerinde bugüne kadar kütlesi olan hiçbir cisim, atom veya elektron, ışık hızına çıkarılamamıştır. Hız arttıkça kütlesi de arttığı için ivmelendirilmesi zorlaşmaktadır.
Galileo ve Lorentz dönüşümleri
Değişik gözlemciler, Newton fiziğinde Galileo dönüşümleri tarafından tanımlanmaktadır. Öncelikle belirli bir O olayı için (x, y, z, t) koordinatlarını kullanan bir K1 referans sistemi düşünelim (örn. yer). Aynı olayın başka bir gözlemci tarafından (x’,y’,z’,t’) koordinatlarıyla ifade edildiğini farz edelim (K2 referans sistemi). Eğer K2, K1 sistemine göre sabit bir hızla x ekseninde hareket ediyorsa (örn. bir tren vagonu) gözlemlenen O için kullanacakları referans sistemleri arasındaki bağıntı şöyle olacaktır:
- x′=x−vt
- y′=y
- z′=z
- t′=t

Bu dönüşümler Newton’un mekanik yasalarına uygulandığında, yasalar formlarını korumaktadır. Fakat aynı şey Maxwell denklemleri için geçerli değildir. Maxwell denklemleri Lorentz dönüşümleri altında ancak formlarını koruyabilmektedir. Lorentz dönüşümleri, Galileo dönüşümlerinden farklı olarak şu şekildedir:
- x′=γ(x−vt)
- y′=y
- z′=z
- t′=γ(t−vxc2)
Ayrıca ters halleri:
- x=γ(x′+vt′)
- y=y′
- z=z′
- t=γ(t′+vx′c2)
burada γ≡11−v2/c2.
Lorentz Dönüşümlerinde görüldüğü üzere iki gözlemci için aynı zaman betimlemesi geçerli değildir. Bu dönüşümlerde Einstein’ın Özel Görelilikle ortaya çıkardığı düşünce değişimi görülmektedir, yani farklı hızlardaki iki gözlemci aynı olay için farklı zaman değerleri ölçer.
Bu dönüşümleri y ve z eksenlerinde de düşünüp yöney (vektör) gösterimi kullanılabilir. Bunun için konumu hıza paralel ve hıza dik olacak şekilde iki bileşene ayırabiliriz:
- r=r⊥+r‖
Bu biçimde sadece hıza paralel bileşen olan r‖ dönüşüme uğrar. O halde, Lorentz dönüşümleri
- r′=r⊥+γ(r‖−vt)
- t′=γ(t−1c2v⋅r)
biçimine indirgenmiş olur.
Dört boyutlu uzay zaman
Minkovski uzayzamanı, özel göreliliğin dört boyutlu yapısını matematiksel olarak betimleyen geometridir. Bu geometride yöneyler (vektörler) dört bileşene sahiptir. Örneğin Öklid uzayında bir konum yöneyi
- r=(x,y,z)
olarak ifade edilir. Özel görelilikte ise “uzayzaman”da bir “konum”u, daha doğru bir deyişle, bir “olay”ı ifade etmek için dörtyöneyler kullanılır. Bu durumda dörtkonum yöneyi,
-
R =(ct,x,y,z) =(ct,r)
olarak tanımlanır. Burada dördüncü bileşen olan zamanın ct şeklinde konulması sadece yöneyin her bileşeninin biriminin metre olması içindir. Çoğu kaynak c=1 seçerek daha sade bir biçim verir. Aynı şekilde dörthız yöneyi de, hızın tanımından
-
U =dRdτ =(cdtdτ,dxdτ,dydτ,dzdτ) =γ(c,ux,uy,uz) =γ(c,u)
olarak çıkarsanır. Buradaki τ özel zamandır.
Aynı şekilde dörtmomentum da,
-
P =m0U =γm0(c,ux,uy,uz) =(mc,mux,muy,muz) =(mc,p) =(E/c,p)
olarak bulunur.
Bu uzayzamanda bir dörtyöneyin boyu,
- V2=v02−v12−v22−v32
olarak tanılandığından, dörthız yöneyinin boyu
- U2=c2
olarak bulunur. Yine, dörtmomentumun boyu
- P2=E2/c3−p0
Ayrıca dörtmomentumun boyu
- P2=m02U2=m02c2=E02/c2
olarak da hesaplanabildiğinden, bu iki sonuç birleştirilip her taraf c2 ile çarpıldığında
- E2=p2+E02
gibi özel göreliliğin en önemli denklemlerinden biri elde edilmiş olunur.
|
Albert Einstein
|
|
|---|---|

1947’de Einstein
|
|
| Doğum | 14 Mart 1879 Ulm, Alman İmparatorluğu |
| Ölüm | 18 Nisan 1955 (76 yaşında) Princeton, New Jersey, Amerika Birleşik Devletleri |
| Ölüm sebebi | Abdominal aort anevrizması |
| Milliyet | Yahudi[1] |
| Vatandaşlık |
|
| Eğitim | ETH Zürih Zürih Üniversitesi Alte Kantonsschule Aarau |
| Evlilikler |
Mileva Marić (e. 1903–1919)
Elsa Einstein (e. 1919–1936)
|
| Çocuk(lar) |
|
| Ödüller |
|
| Kariyeri | |
| Dalı |
|
| Çalıştığı kurumlar |
|
| Doktora danışmanı |
Alfred Kleiner |
| Etkilendikleri |
|
| Etkiledikleri | Hemen hemen tüm modern fizikçiler |
| İmza | |
|
|
|
Albert Einstein (/ˈaɪnstaɪn/; Almanca telaffuz: [ˈalbɛɐ̯t ˈaɪnʃtaɪn]; 14 Mart 1879, Ulm – 18 Nisan 1955, Princeton), en çok görelilik kuramını geliştirmesiyle tanınan Almanya doğumlu teorik fizikçi ve bilim insanı. Einstein, kuantum mekaniğine de önemli katkılarda bulundu. Özel görelilikten kaynaklanan kütle-enerji denkliği formülü E = mc2, “dünyanın en ünlü denklemi” olarak adlandırıldı. Teorik fiziğe yaptığı hizmetlerden ve özellikle fotoelektrik etki yasasını keşfetmesinden dolayı 1921’de Nobel Fizik Ödülü’nü aldı.
Alman İmparatorluğu’nda doğan Einstein, 1895 yılında İsviçre’ye taşındı ve ertesi yıl Alman vatandaşlığını bıraktı. 1897 yılında, on yedi yaşındayken Zürih’teki İsviçre Federal Politeknik Okulu’nda matematik ve fizik öğretmenliği diploma programına kaydoldu ve 1900 yılında mezun oldu. Bir yıl sonra İsviçre vatandaşlığına geçti ve ardından Bern’deki İsviçre Patent Ofisi’nde kalıcı bir pozisyon elde etti. 1905 yılında Zürih Üniversitesi’ne başarılı bir doktora tezi sundu. 1914’te Prusya Bilimler Akademisi ve Berlin Humboldt Üniversitesi’ne katılmak üzere Berlin’e taşındı ve Kaiser Wilhelm Fizik Enstitüsü’nün müdürü oldu. 1933 yılında Einstein, Amerika Birleşik Devletleri’ni ziyaret ederken Almanya’da Adolf Hitler iktidara geldi. Yahudi dostlarına yönelik Nazi zulmünden dehşete düşen Einstein, ABD’de kalmaya karar verdi ve 1940 yılında Amerikan vatandaşlığına kabul edildi. İkinci Dünya Savaşı arifesinde Başkan Franklin D. Roosevelt’e bir mektup yazarak onu potansiyel Alman nükleer silah programı konusunda uyardı ve ABD’nin de benzer araştırmalara başlamasını tavsiye etti.
1905 yılında, annus mirabilis (mucize yılı) olarak da tanımlanan çığır açan dört makale yayınladı.[5] Bu makaleler fotoelektrik etki teorisinin ana hatlarını çizdi, Brown hareketini açıkladı, özel görelilik teorisini tanıttı ve özel teori doğruysa kütle ve enerjinin birbirine eşit olduğunu gösterdi. 1915 yılında mekanik sistemini kütleçekimi de içerecek şekilde genişleten bir genel görelilik kuramını ortaya attı. Ertesi yıl yayınladığı kozmolojik bir makale, evrenin bir bütün olarak yapısının ve evriminin modellenmesi için genel göreliliğin sonuçlarını ortaya koydu. 1917’de Einstein, spontane emisyon ve uyarılmış emisyon kavramlarını tanıtan, ikincisi lazer ve mazerin arkasındaki temel mekanizma olan ve daha sonra kuantum elektrodinamiği ve kuantum optiği gibi fizikteki gelişmeler için faydalı olacak bir bilgi hazinesi içeren bir makale yazdı.[6] 1935’te fizikçi Nathan Rosen ile ortak bir makalede solucan deliği kavramını ortaya attı. Fizikçi Leó Szilárd ile birlikte, hareketli parçası olmayan ve girdi olarak sadece ısı kullanan bir buzdolabı icat etti.
Yaşamı
Alman İmparatorluğu’nun Ulm kentinde, Aşkenazi Yahudi bir ailede dünyaya gelen Einstein, yaşamının ilk yıllarını Münih’te geçirdi. Lise eğitimini ve yüksek eğitimini İsviçre’de tamamladı; fakat bir üniversitede iş bulmada yaşadığı zorluklar nedeniyle bir patent ofisinde müfettiş olarak çalışmaya başladı. 1905 yılı Einstein için bir mucize yıl oldu ve o dönemde kuramları hemen benimsenmemiş olsa da ileride fizikte devrim yaratacak olan dört makale yayımladı. 1914 yılında Max Planck’ın kişisel ricası ile Almanya’ya geri döndü. 1921 yılında fotoelektrik etki üzerine çalışmaları nedeniyle Nobel Fizik Ödülü’ne layık görüldü. Nazi Partisi’nin iktidara yükselişi nedeniyle 1933’te Almanya’yı terk etti ve Amerika Birleşik Devletleri’ne yerleşti. Ömrünün geri kalanını geçirdiği New Jersey eyaletinin Princeton ilçesinde ölmüştür.
Albert Einstein, özel görelilik ve genel görelilik kuramları ile iki yüzyıldır Newton mekaniğinin hakim olduğu uzay anlayışında bir devrim yaratmıştır. Sadece matematik hesaplamalar ve denklemler ile oluşturduğu kuramları sonradan deneysel olarak defalarca doğrulanmıştır. E = mc2 denklemi ile formüle ettiği kütle-enerji eşdeğerliği yıldızların nasıl enerji oluşturduğuna açıklama getirmiş ve nükleer teknolojinin önünü açmıştır. Fotoelektrik etki ve Brown hareketine getirdiği matematiksel açıklamalar, modern fiziğe diğer katkıları arasındadır. Ömrünün büyük bir kısmını bütün kuramları birleştiren bir birleşik alan kuramı yaratmaya çalışarak geçirmiş ama bu çabaları sonuçsuz kalmıştır. Einstein kuantum mekaniğinin bazı sonuçlarına, özellikle belirsizlik ilkesine oldukça şüpheci yaklaşmış fakat bu yaklaşımlar ileride geniş kabul görmüştür.
Einstein, Nazilerin nükleer bomba geliştirmesi endişesiyle ABD başkanı Franklin D. Roosevelt’e bir mektup göndermiş, ABD’nin nükleer çalışmalara başlamasını tavsiye etmiştir. Holokost sonrası Yahudilerin kendi ülkelerine sahip olması gerektiği fikrini savunmuş, İsrail’in kuruluşuna destek vermiştir. Çeşitli söyleşilerinde Yahudilik dinine ve diğer kutsal kitaplara inanmadığını belirtmiş, sosyalizme sempati duyan bir makale yayımlamıştır. Bertrand Russell ile birlikte nükleer silahlara karşı bir manifesto da yayımlamıştır.
1999’un sonlarında 100 ileri gelen fizikçiyle gerçekleştirilen milenyum oylamasında Einstein, tüm zamanların en iyi fizikçileri arasında 1. sırayı almıştır.[7][8]
Einstein, hayatı boyunca 300’den fazla bilimsel makale yayımlamıştır, ayrıca 150’den fazla bilim dışı çalışmaları da olmuştur. Başarıları ve eserleri nedeniyle Einstein sözcüğü, “dâhi” ile eş anlamlı olarak kullanılmaya başlanmıştır.
Çocukluğu ve eğitimi

Albert Einstein 14 Mart 1879’da Almanya’nın Ulm kasabasında dünyaya geldi.[9] 1880 yazında ailesi Münih’e taşındı.[9] Münih’te babası Hermann Einstein ve amcası Jakob bir elektrik şirketi kurdular. Annesi Pauline Einstein yetenekli bir piyanistti.[10] Albert iki buçuk yaşındayken kız kardeşi Maja dünyaya geldi. Okula başlamadan önce konuşma zorlukları yaşıyordu, annesi ve babası kaygılanarak onu doktora götürmüşlerdi.[11]
Dört beş yaşlarında hasta bir şekilde yataktayken babası neşelendirmek için ona manyetik bir pusula vermişti. Pusula ibresinin hareketini o yaşta oldukça gizemli bulmuştu ve kendinde büyük bir merak uyandırmıştı.[12]
Hermann ve Pauline Einstein Yahudi kökenli bir çiftti fakat dindar değillerdi.[10] Yapılması gereken dini etkinliklerinden daha çok çocuklarının eğitimini düşünüyorlardı. Einstein beş yaşına geldiğinde onu evlerinin yakınlarında daha iyi eğitim verdiğini düşündükleri bir Katolik Hristiyan ilkokuluna yazdırdılar.[13] Einstein okula başladıktan sonra okuldaki sıkı disiplinden ve ezberci anlayıştan rahatsız olmaya başlamıştı.[14] Ama okul ile hoşnutsuzluğuna rağmen yüksek notlar alıyordu. Birinci sınıfı atlamıştı ve çoğu dönemde sınıfında birinci olmuştu.
Einstein’ın annesi Pauline çocuklarının erken yaşta müzik ile tanışmalarını istiyordu. Pauline Albert’ı keman derslerine, kız kardeşi Maja’yı ise piyano derslerine göndermişti. Albert keman derslerine altı yaşında başladı ve on dört yaşına kadar devam etti.[15] Mozart’ın sonatlarını çok beğendi ve onları çalabilmek için tekniğini geliştirmek istedi. Sonunda iyi bir amatör kemancı olmuştu ve Mozart, Beethoven sonatları çalmaktan hoşlanıyordu.[16]
Einstein dokuz buçuk yaşındayken Katolik ilkokulundan ayrıldı ve Luitpold Gymnasium’da eğitim görmeye başladı.[17] Gymnasium Antik Yunanca ve Latinceye büyük önem veriyordu.[18] Müfredatta ayrıca modern diller, coğrafya, edebiyat ve matematik de bulunuyordu. Einstein Latince ve matematikteki keskin mantığı seviyor ve bu derslerde en yüksek notları alıyordu. Gymnasium ilkokuldan çok daha sıkı bir disipline sahipti.[11] Einstein burada otoriter öğretmenler ile sürekli çatışıyordu ve öğretmenleri Einstein’ın bağımsız, isyankar kişiliğinden hiç hoşlanmıyordu.[11]

Einstein’ın ailesi, eski bir Yahudi geleneği olarak yoksul bir öğrenciyi evlerinde yemeğe davet ediyordu.[19] Max Talmud isminde yoksul bir Yahudi üniversite öğrencisi her hafta bir akşam yemeğine katılıyordu.[11] Talmud’un ziyaretleri Einstein on yaşındayken başlamıştı ve beş yıl boyunca sürmüştü. Einstein kendinden büyük bir üniversite öğrencisi ile konuşmaktan hoşlanıyordu ve Talmud kısa sürede Einstein’ın sıradan bir çocuk olmadığını sezmişti. Birlikte bilim, matematik ve felsefe konuşuyorlardı.[11] Einstein on üç yaşındayken, Talmud Immanuel Kant’ın Saf Aklın Eleştirisi kitabını getirdi. Einstein o yaşta kitabı anlamakta hiç zorlanmamış ve okulunda sürekli Kant hakkında konuşmaya başlamıştı.[11]
Talmud, Einstein’a sürekli çeşitli popüler bilim kitapları getiriyordu ve Einstein hepsini büyük bir heves ile inceliyordu.[11] Bir keresinde Talmud, Öklid’in Elemanlar kitabını getirdi.[11] Einstein kitaptaki problemler üzerinde çalışmaya başladı. Yaz bitmeden önce Einstein sadece bütün problemleri çözmek ile kalmamış, ayrıca teoremlere alternatif ispatlar da bulmuştu.
Einstein on bir yaşındayken Yahudi geleneği olarak evde din dersleri almaya başlamıştı.[15] Einstein bu dönemde büyük bir dini istek duymaya başladı ve bütün dini gerekleri yerine getirerek dindar olmayan ailesine örnek olmak istiyordu. Şabat günü dinleniyordu, sadece Yahudiler için helal olan gıdaları yiyordu, kendi başına dini şarkılar yazmıştı.[19] Ama Einstein’ın dini isteği uzun sürmedi. Bir yıl içerisinde okuduğu bilimsel kitapların kutsal kitaplar ile çeliştiğini gördü. Sonrasında her çeşit otoriteden kuşku duymaya başladı ve kuşkucu bir tavır geliştirdi.[19]
1891 yazında mühendis amcası Jakob kendine bir cebir kitabı getirmişti. Einstein o yaz cebir kitabına çalışmaya karar verdi ve amcasından çözmek için problemler istedi. Einstein en zor ve karmaşık problemleri bile çözebiliyordu. O yaz, Einstein Pisagor teoreminin tekrar bir ispatını yaptı. Cebir ve geometriden sonra Einstein kalkülüse yöneldi. On altı yaşına geldiğinde kendi başına diferansiyel ve integral hesaplamaları ile analitik geometriyi öğrenmişti.[11]
1894’te Einstein’ın babası ve amcasının şirketi 14 yılın ardından iflas etti. İki aile birlikte İtalya’ya gitmek ve şanslarını orada denemek istediler.[9] Ailesi Albert’ın Münih’te kalıp okulunu Gymnasium’da bitirmesine karar verdi. Bu sırada Einstein on beş yaşındaydı ve liseyi bitirmesine daha üç yıl vardı. Münih’te tek başına altı ay geçirdikten sonra Einstein bunalıma girdi ve gerginleşmeye başladı. Aile doktorunu ikna ederek sinir sorunları nedeniyle kendinin ailesinin yanında bulunması gerektiğini belirten bir rapor aldı. Einstein ailesine haber vermeden Gymnasium’dan ayrıldı ve İtalya’daki ailesinin yanına geldi.[20]
İsviçre’deki eğitimi
Einstein, İtalya’ya geldiğinde teknik olarak bir lise terk olsa da, eğitimini yarıda bırakma niyeti yoktu. Ailesine Zürih, İsviçre’deki Federal Politeknik Okulu’na girmek için tek başına ders çalışacağına söz verdi. Politeknik kabul için bir lise diploması istemiyordu. Einstein’ın tek yapması gereken kabul sınavlarını geçmekti. Einstein için İtalya’da yaşam oldukça rahattı. Ders çalışmayı İtalya’yı gezmek ile birleştirdi, pek çok müze ve sanat galerisi gezdi.
Einstein, Almanya’nın militarizminden ve sıkı disiplininden hiç hoşlanmıyordu, zorunlu askerlik yapmak da istemiyordu. Babasına Almanya vatandaşlığından çıkmak istediğini ve İsviçre vatandaşı olmak istediğini söyledi. Babası biraz tereddüt ile onayladı ve gerekli kâğıtları imzaladı. 28 Ocak 1896’da Einstein kendini Almanya vatandaşlığından çıkaran resmi kâğıtları aldı ama 1901 yılına kadar İsviçre vatandaşlığını almadı. Beş yıl boyunca Einstein vatansızdı.[21]
Einstein, 1895 Ekim’inde Zürih’e gitti ve Politeknik’te kabul sınavına girdi. Sınava girmek için on sekiz yaş üstü olmak gerekiyordu ve on altı yaşında girebilmesi için özel bir izin almıştı.[22] Einstein babasının tavsiyesine uyarak mühendislik bölümüne başvurdu. Kabul sınavında matematik ve fizikte çok üstün dereceler aldı ama diğer bölümlerde başarısız olmuştu.[22] Politeknik’in yöneticisi Einstein’ın potansiyelini görmüştü ve onun bir İsviçre lisesinde diploma alıp tekrar başvurmasını tavsiye etti. Einstein’ın ailesi Politeknik’in önerisini kabul ederek Einstein’ı İsviçre’nin Aarau bölgesinde bir liseye gönderdiler.[9] Bu yıllar belki de Einstein’ın gençliğinin en güzel yıllarıydı. Zürih’ten 30 km uzaklıktaki bir köyde bulunan lise Einstein için idealdi. Saygı duyulan, açık fikirli bir öğretmen olan Jost Winteler tarafından yönetiliyordu.[11] Okulda rahat bir ortam vardı ve öğrencilerin bağımsız düşünmesi teşvik ediliyordu. Bu yaklaşım Einstein’ın kişiliğine uyuyordu. 1896’da Aarau okulunda yüksek notlar ile final sınavlarını geçti.[11]
Einstein mezun oldu ve gerekli yaştan altı ay küçük olmasına rağmen Politeknik’e kabul edildi.[9] Einstein ile birlikte yaklaşık bin yeni öğrenci o sene Politeknik’te eğitime başlamıştı. Çoğu öğrenci mühendislik okullarına katılmıştı ama Einstein fiziği tercih etti. Fizik departmanı büyük ve modern bir binadaydı ve çok iyi ekipmana sahipti. Fakülte dünya standartlarındaydı. Adolf Hurwitz ve Hermann Minkowski gibi ünlü matematikçiler, Einstein’ın profesörleri arasındaydı.[23] Einstein’ın o dönemdeki yaşamı tipik bir Avrupalı üniversite öğrencisi hayatıydı. Kafeler ve barlarda uzun saatler harcıyordu. Kahve içerek arkadaşları ile bilim ve felsefe tartışıyordu. Hangi derslere odaklanması gerektiği konusunda seçiciydi. Eğer konuyu ya da profesörü beğenmiyorsa o derslere girmiyordu.[22] Politeknik’te öğrenciler dört sene boyunca sadece iki dönem sonunda sınavlara giriyordu. Bunlar dışında not kaygısı ya da yoklama kaygıları yoktu. Einstein aldığı dersler ile hiçbir alakası olmayan, sadece ilgi duyduğu kitapları çalışıyordu. Politeknik’te profesörlerin her biri araştırmacıydı ve ders kitapları yerine kendi araştırmalarını izliyorlardı. Ders notu hiç tutmayan Einstein, hayat boyu arkadaşı kalacak olan Marcel Grossman’ın titizlik ile tuttuğu ders notları sayesinde sınavları başarılı bir şekilde geçebilmişti.[24]
Einstein Politeknik’te ileride eşi olacak olan Mileva Marić ile tanıştı. 1896’da bir dönem eczacılık okuduktan sonra fizik bölümüne geçmişti. Einstein’ın ilk senesinde sınıf arkadaşıydılar ve bu dönemde ikisi arasında romantik bir ilişki başlamıştı. Üniversitedeki son senelerinde evlenmeye karar verdiler. Einstein ve Mileva çoğu zaman birlikte fizik çalışıyor, kitaplar inceliyor ve tartışıyorlardı.[25] Mileva Maric’in Einstein’ın ilerideki makalelerine katkıları olduğu iddia edilmiş olsa da bu iddialara yönelik kanıt bulunamamıştır.[26]
Çiftin üçüncü senesinde Einstein, Profesör Heinrich Weber’in elektroteknik laboratuvarı dersini aldı. Derste sadece zorunlu deneyleri değil, kendi tasarladığı deneyleri de yapıyordu. Sadece laboratuvarda kendi çalışmalarını yapmak için başka bazı derslere girmediği oluyordu. Einstein Weber’in fiziğe giriş derslerini beğeniyordu ama daha ileri fizik konularındaki derslerini yetersiz bulmuştu. Weber Maxwell’in elektromanyetik kuramı hakkında hiç konuşmuyordu.[11] Einstein bu dönemde saygısız ve ukala olmaya başlamıştı ve bu tavrının cezasını mezuniyet sonrası çekecekti. Weber Einstein’ın üniversitede akademik bir pozisyona yerleşmesine engel olmuştu. Weber’in elektrik ve manyetizma derslerinden hayal kırıklığına uğrayan Einstein, bu konuları kendi başına çalışmaya karar verdi. Elektromanyetizma konusunda pek çok kitap edindi ve bunları kendi başına çalıştı. Bu dönemde Einstein ayrıca o dönemde oldukça yaygın olan esir fikri hakkında kuşkucu bir şekilde düşünüyordu.
1900 yılında Einstein üniversiteden fizik diploması ile mezun oldu. Üniversitede bir asistanlık pozisyonu bulmak istiyordu, böylece doktorası için araştırma yapabilecekti. Fakat üniversite yıllarında pek çok profesörünü isyankar tavırları ile kızdırmıştı.[24] Profesörleri ayrıca Einstein’ın derslere girmemiş olmasından, kendi istediği konuları çalışmasından hoşlanmamıştı. Profesörler tavsiye mektuplarını yazdıktan sonra Einstein Politeknik’te bir pozisyon bulamadı. Başka üniversitelerde, kendi araştırma makalelerini göndererek pozisyonlar aradı ama hiç olumlu yanıt alamadı.
Bern Patent ofisi

Mezun olduktan sonra Einstein iki yılını sıkıntılı bir şekilde bir öğretmen işi bulmak için harcadı. Eski bir sınıf arkadaşının babası kendine Bern’de bir patent ofisinde, asistan müfettiş olarak iş buldu.[27] Elektromanyetik cihazlar için patent başvurularını inceledi.
Patent ofisinde işinin büyük kısmı elektrik sinyallerinin aktarımı ve elektriksel-mekanik zaman eşgüdümü ile ilgili sorular hakkındaydı. İki teknik soru hakkında yaptığı düşünce deneyleri, Einstein’ın ışığın doğası ile zaman, uzay ve zamanın ilişkisi hakkında kökten sonuçlara varmasını sağlamıştır.
Bern’de tanıştığı birkaç arkadaşı ile adını mizahi bir şekilde “The Olympia Academy” koydukları küçük bir tartışma grubu oluşturmuş, bilim ve felsefe hakkında tartışmak için düzenli olarak buluşuyorlardı. Okudukları arasında Henri Poincare, Ernst Mach ve David Hume vardı; bu adlar kendinin bilimsel ve düşünsel bakış açısını oldukça etkilemişlerdir.[kaynak belirtilmeli]
1909’da patent ofisindeki işinden ayrılmış ve Zürih Üniversitesi’nde kuramsal fizik profesörü olmuştur.

Mileva Maric ile evliliği
[değiştir | kaynağı değiştir]
Politeknik’ten sınıf arkadaşı Mileva, hamile olduğu için eğitimini yarım bırakmak zorunda kalmış ve 1902’de Novi Sad’a ailesinin yanına giderek bir kız çocuğu dünyaya getirmişti. Lieserl adı verilen kızlarının akıbeti meçhuldür; hastalanarak ölmüş veya evlatlık verilmiş olabilir.[28] Albert Einstein Bern Patent ofisinde çalışmaya başladığı sırada Mileva yanına geldi ve çift evlendi (1903). Bu evlilikten Hans Albert (d. 1905) ve Eduard (d.1909) adlarında iki oğlu dünyaya geldi. Einstein’in 1912’de teyzesinin kızı Elsa Loewenthal ile yaşamaya başladığı ilişki üzerine Mileva ile evliliği bozuldu; 1914’te ayrı yaşamaya başlayan eşinden 1919’da boşandı.
Annus Mirabillis
1905, Einstein’ın hayatının en verimli yılı olmuştur ve bu yıla “annus mirabillis” (Latince: “mucizevi yıl”) denmektedir. Bir yıl içerisinde Annalen der Physik (Fizik Yıllıkları) dergisinde yayımladığı dört makale, modern fizik anlayışında devrim yaratmıştır. Bu makaleler:

| Yayın Tarihi | Almanca | Türkçe | Konu | Önemi |
|---|---|---|---|---|
| 9 Haziran | Über Einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt | Işığın Oluşumu ve Dönüşümü Üzerine Bir Görüş | Fotoelektrik etki | Planck’ın “Kara Cisim Işıması” çıkmazına çözüm olarak önerdiği, radyasyonun kuantalardan oluştuğu tezinin ışık için de geçerli olduğunu önerdi ve böylece kuantum kuramının temellerinin atılmasına önemli bir katkı sağladı. |
| 17 Temmuz | Über die von der molekularkinetichen Theorie der Wärme geoforderte Bewegung von ruhenden Flüssigkeiten suspendierten Teilchen | Durağan Bir Sıvı İçindeki Asıltı Parçacıklarının Moleküler Kinetik Kuramı Çerçevesindeki Hareketleri Üzerine | Brown hareketi | Atomların varlığına bir kanıt sundu ve istatistik fizik alanına destek sağladı. |
| 26 Eylül | Zur Elektrodynamik bewegter Körper | Hareketli Cisimlerin Elektrodinamiği | Özel görelilik | Maxwell’in elektromanyetik denklemleri ile mekanik yasalarını bağdaştırdı, ışık hızının her referansa göre sabit olduğunu önerdi, esirin varlığını reddetti. |
| 21 Kasım | Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? | Bir Cismin Eylemsizliği Enerji İçeriğine Bağlı mıdır? | Kütle-enerji eşitliği | Kütle enerji eşitliği adlı ünlü formülünü ortaya koydu. |
Akademik kariyeri
1908’de artık oldukça tanınmış, büyük bir bilim insanı olarak tanınıyordu ve Bern Üniversitesine öğretim üyesi olarak atanmıştı. Sonraki sene patent ofisindeki işinden ve öğretim üyeliğinden ayrıldı ve Zürih Üniversitesinde fizik doçentliğine başladı. 1911 yılında Prag’da Karl-Ferdinand Üniversitesinde (günümüzde Prag Üniversitesi) profesörlük unvanı aldı. 1914 yılında Almanya’ya döndü, Kaiser Willhelm Fizik Enstitüsü’nde yönetici, Berlin Humboldt Üniversitesinde profesör oldu. Bu işlerindeki sözleşmelerinde öğretmenlik görevlerini oldukça azaltan maddeler vardı.
Prusya Bilim Akademisinin bir üyesi olmuştur. 1916 yılında Einstein Deutsche Physikalische Gesellschaft (Alman Fizik Derneği)’ın başkanı olmuştur (1916-1918).
1911 yılında, yeni genel görelilik kuramına göre, başka bir yıldızın ışığının güneş tarafından kırılacağını hesaplamıştır. Bu tahmini sonradan Arthur Stanley Eddington’un 1919’daki güneş tutulması gözleminde doğrulanmıştır. Bu olayın uluslararası basında haberleşmesi, Einstein’ı dünyaca ünlü yapmıştır.
1921 yılında Einstein Nobel Fizik Ödülü’ne layık görülmüştür. O dönemde görelilik hâlâ tartışmalı görüldüğü için, ödül fotoelektrik etkisini açıklaması nedeniyle verilmiştir. 1925 yılında da Royal Society tarafından Copley Medal almıştır.

Elsa Einstein ile evliliği
Mileva Maric ile evliliği sırasında kuzeni Elsa ile bir aşk ilişkisi yaşayan Einstein, 1919’da Mileva’dan boşandıktan birkaç ay sonra onunla evlendi. Çiftin çocukları olmadı ama Einstein Elsa’nın önceki evliliğinden olma Ilse ve Margot adlı iki kızını kendi kızları olarak benimsedi. Aile, ABD’ye göçene kadar Berlin’de yaşadı; yazları ise Potsdam yakınındaki yazlıklarında geçirdi.[29]
Amerikan vatandaşlığı ve Princeton, New Jersey
Einstein, Nisan 1933’te Amerikan üniversitelerini ziyaret ederken, Alman hükûmetinin Yahudileri üniversitelerde öğretmenlik dahil bütün resmi konumlardan men ettiğini öğrendi. Bir ay sonra Naziler kitap yakma kampanyalarına başladı ve Einstein’ın eserleri de yakılanlar arasındaydı. Einstein bu gezisinde Almanya’ya bir daha geri dönmeyeceğini söyledi.
Mart 1933’te Avrupa’ya döndüğünde birkaç ay Belçika’da kaldı, sonrasında geçici olarak İngiltere’ye geçti. Aynı yıl ABD’ye göç etmeye karar verdi. Princeton, New Jersey’de, Institute for Advanced Study’de görev aldı ve 1955’te ölümüne kadar burada kaldı. Burada kendi bir birleşik alan kuramı geliştirmeye ve kuantum fiziğinin kabul edilmiş yorumlarını çürütmeye çalıştı. Bu iki girişimi de başarısız oldu.
Manhattan Projesi

1939 yılında, fizikçi Leo Szilard dahil bir grup Macar bilim insanı Nazilerin atom bombası araştırmaları konusunda Washington’u uyardı. Grubun uyarısı ciddiye alınmadı. 1939 yazında, Avrupa’da İkinci Dünya Savaşı başlamadan birkaç ay önce, Einstein prestijini kullanarak Leo Szilard ile birlikte, Başkan Roosevelt’e, Nazi Almanya’sının atom bombası tehlikesine karşı uyarı mektubu gönderdi. Aynı mektupta Amerikan hükûmetinin uranyum araştırmaları ve zincir reaksiyonları ile ilgili araştırma yapması tavsiye ediliyordu. Einstein ve diğer mülteci arkadaşları “Alman bilim adamlarının atom bombası yarışını kazanabileceği ve Hitler’in bu silahı kullanmak için oldukça istekli olacağı” konusunda uyarıyordu.

Mektubun ABD hükûmetinin savaş öncesi nükleer silahlar hakkında yoğun araştırma yapmasının önemli bir tetikleyicisi olduğu düşünülmektedir. Başkan Roosevelt, Hitler’in önce atom bombasına sahip olması riskini üstlenemezdi. Einstein’ın mektubu ve buluşmaları sonucu ABD bombayı geliştirme yarışına girdi. Savaş sırasında ABD bombayı geliştirebilen tek ülke oldu.
1954 yılında, ölümünden bir yıl önce, bu konuda arkadaşı Linus Pauling’e şunları söylemiştir. “Hayatımda tek bir büyük hata yaptım. Başkan Roosevelt’e atom bombası tavsiyesini yapmak. Ama yine de bir nedeni vardı. Almanların daha önce yapması tehlikesi”.
Ölümü ve beyninin çalınması
18 Nisan 1955’te, Albert Einstein iç kanama geçirdi. İsrail’in kuruluşunun yedinci yıl dönümü nedeniyle bir televizyon konuşmasının taslağını hazırlıyordu ama bu çalışmasını bitiremeden öldü. Einstein ameliyatı şu sözlerle reddetti, “İstediğim zaman gitmek istiyorum. Hayatı yapay bir şekilde uzatmak tatsız. Ben payımı kullandım, şimdi gitme zamanı ve bunu zarif bir şekilde yapmak istiyorum”. 76 yaşında, Princeton Hastanesi’nde gece saat 01.55’te öldü.
Otopsisi sırasında Princeton Hastanesi patolojisti Thomas Stoltz Harvey o gece nöbetteydi ve Einstein’ın ölüm nedenini belirlemesi gerekiyordu. Beyni kafatasından çıkardıktan sonra kendi kendine “Bu dünyamız hakkında her şeyi değiştiren beyindir” demiştir. Einstein öldükten sonra vücudunun putlaştırılarak tapılmasını istemiyordu. Fikirlerine ve bilime olan katkısına odaklanması gerektiğine inanıyordu. Bunun için ailesi tarafından öldükten sonra yakılması fikri ortaya atıldı. Harvey bedeni yakılması için hazırladı. Beyni ise kendi sefer tasına koydu ve evine götürdü. Böylece Einstein’ın beyni çalınmış oldu.
Beyni çalınan Einstein’ın ailesi şoktaydı. Hükûmet yetkileri ve Harvey’in meslektaşları ise çileden çıkmıştı. Herkes beynin iade edilmesini istiyordu ancak Harvey bunu kabul etmedi. Bu nedenle de işinden oldu. Ancak Harvey beyni bilimsel araştırmalarda kullanılacağına yemin edince, ailesi bu isteğinden vazgeçti. Daha sonra Einstein’ın kalıntıları ailesi tarafından yaktırıldı ve külleri bilinmeyen bir yere serpildi. Beyni ise Harvey tarafından 1985 yılına kadar hayatının anlamı oldu ve bu yılda beynin bir kısmını o yıllarda beyinle uğraşan bir uzmana gönderdi. Gönderdiği uzman tarafından bulunanlar ise basında bir sansasyona neden oldu. Çalışmalar Einstein’ın beyninde bulunan ve beyin nöronlarını besleyen glial hücrelere odaklanmıştı. Einstein’ın beyninde normal bir insana nazaran daha fazla glial hücre bulunuyordu. Fakat bu konuda bilim adamları farklı fikirler ortaya attılar.
Einstein’ın beyni 53 yıl sonunda çalındığı Princeton Hastanesi’ne geri döndü. Harvey bundan 3 yıl sonra hayatını yitirdi.
Bilimsel çalışmaları
Özel görelilik kuramı
19. yüzyılın sonlarında Michelson-Morley deneyi, ses ve başka dalga olaylarının tersine, ışık hızının referans sistemine göreceli olmadığını göstermişti.[27] O dönemde sesin hava aracılığıyla yayıldığı gibi ışığın da esir denen gizemli bir ortamda yayıldığı düşünülüyordu.[27]
Einstein, ışık hızının sabit olduğunu ve ışığın yayılması için esir ortamının gerek olmadığını ve mekan zaman ve hareketin izafi olaylar olduğunu düşündü.[30] Çalışmalarının sonucuna varırken iki ilkeyi varsaydı: görelilik ilkesi sabit hızla hareket eden bütün gözlemciler için geçerlidir ve ışığın hızı bütün gözlemciler için c’dir.[31] Einstein’ın kuramı ile sabit hızla hareket eden iki gözlemcinin matematik hesap ile aynı olayın gözlemcilere göre yer ve zamanı belirlenebiliyor.[31] Bu kuram, Newton’un her yerde aynı işleyen, herkes için aynı “mutlak zaman” fikrini yıkıyordu.[31] E=mc² düşüncesinin kökeni bu kuramdır.
Genel görelilik kuramı
Özel görelilik kuramı düzgün, doğrusal ve ivmesiz hareket eden sistemlerle sınırlıydı.[32] Genel görelilik kuramı ise birbirine göre ivmeli hareket eden sistemleri de kapsıyordu. Birinci kuram, kapsamı daha geniş olan ikinci kuramın özel bir hali sayılabilir.[32]
Genel görelilik, gravitasyon kavramına yeni bir bakış açısı getirdi.[32] Klasik mekanikte gravitasyon, kütlesel nesneler arasında çekim gücü olarak algılanıyordu.[32] Örneğin dünyayı yörüngede tutan, kütlesi daha büyük Güneş’in çekim gücüydü.[32] Genel görelilik kuramına göre ise gezegenleri yörüngelerinde tutan, yörüngenin yer aldığı uzay kesiminin Güneş’in kütlesel etkisinde kavisli bir yapı oluşturmasıdır.[32] Genel kuram ayrıca gravitasyon ile eylemsizlik ilkesini “gravitasyon alanı” adı altında birleştirdi.[32]
Kütle-enerji eşitliği
Albert Einstein, enerjinin ışık hızının karesiyle maddenin kütlesinin çarpımına eşit olduğunu bularak kendine kadar süregelen bir yargıyı yıkarak bilim dünyasında yeni bir çığır açmıştır. Ondan öncesinde kütle ile enerji arasında bir bağlantı kurulmamıştır ve ayrı olgular oldukları varsayılmıştır. 19. yüzyılda kimyagerlerin hassas aygıtları olmadığı için kimsenin dönüşüm sonrası kütle kaybından haberleri yoktu. Basit tepkimeler sonrası oluşan kütle kaybı fark edilememişti. Einstein ise bütün bilinenleri yıkarak çağdaş bilimin temel taşlarını atmıştır. Ona göre her şey enerjidir, yani maddeler de çok yoğun enerjilerdir. Kimyasal reaksiyonlar sonrası küçük de olsa kütlenin bir kısmı enerjiye dönüşmektedir. Bu durumu açıklamak için eşitliğin az farklı formülasyonu E=mc² ilk defa Albert Einstein tarafından 1905’te ünlü makalelerinde yayımlanmıştır. Aynı yıl önermiş olduğu özel görelilik kuramının bir sonucu olarak türetmiştir.
Fotoelektrik etki
Einstein öncesinde ışık, kimi bilim adamları tarafından tanecikler akımı, kimileri tarafından da dalga devinimi olarak nitelendirilmişti.[27] 19. yüzyılın başlarında Young’la başlayan, Fresnel ve daha sonra Faraday ve Maxwell’in çalışmalarıyla pekişen deneyler dalga kuramına belirgin bir üstünlük sağlamıştı.[27] Einstein’ın fotoelektrik çalışması, bu gelişmeyi tersine çevirmiş, hem de Planck’ın 1900’de ortaya sürdüğü kuantum teorisini de çarpıcı bir biçimde doğrulamıştır.[27]
Üzerine ışık düşen bazı maddeler elektron salıyorlardı. Parlak ışıklar daha fazla elektron salıyor fakat enerjileri artmıyordu. Sarı ve kırmızı ışıklar pek az elektron salıyorlardı. Klasik fizik bu durumu dalga kuramı ile açıklayamıyordu. Einstein bu soruna Planck kuramını uyguladı. Sonradan foton adı verilen belirli enerjili bir kuanta, maddenin atomu tarafından soğrulmakta, böylece belirli enerjide bir elektron atomdan alınmaktadır.
Einstein bu çalışması sayesinde 1921 yılında Fizik Nobel Ödülünü kazanmıştır.
Brown hareketi ve istatistiksel fizik
1850’lerde İngiliz botanikçisi Robert Brown, mikroskoplarla polenleri incelerken, taneciklerin su içinde rastgele sıçramalarla devinim içinde olduğunu gözlemledi; fakat bu gözlem 1905’e dek açıklamasız kaldı.[27] Molekül kavramı yeni değildi; ancak en güçlü mikroskop altında bile görülemeyecek kadar küçük olan moleküllerin varlığı, ilk kez bu açıklamayla kanıtlanmış oldu.[27]
Brown’a göre asıltının içinde bulunduğu su, Maxwell ve Boltzman kinetik kuramı çerçevesinde hareket eden moleküllerden oluşuyorsa asıltı parçacıklar gözlendiği gibi titreşirler.[13] Su içindeki bütün cisimler her yönden ve sürekli olarak moleküllerle itilirler.[13]
Einstein hareket ile molekül büyüklüğü arasındaki matematik ilişkiyi saptamış ve böylece molekül ve atomların büyüklüğünü hesaplamak mümkün olmuştu.[13] Bu açıklamadan üç yıl sonra Perrin, Brown hareketi üzerinde deneyler yaparak Einstein’ın hesaplarını doğruladı.[13]
Bose-Einstein istatistiği
Einstein ve Hint fizikçi Nath Bose, 1925’te yoğun bir gaz kütlesinin mutlak sıfır sıcaklığına düşürüldüğünde, atomlar kendi özelliklerini kaybedecek, bir bütün halinde dev bir tek atoma dönüşecekleri sonucuna vardılar.[33] Bose’un fotonlar için kullandığı metotları ayırt edilemez parçacıklar için genelleştiren Einstein, yaptığı çalışmalarda etkileşmeyen parçacıklardan oluşan bozon gazının tek bir kuantum durumuna yoğuşabileceğini göstermiştir.[34]

Kuantum fiziği ve belirsizlik ilkesi
1930 yılında belirlenemezlik ilkesinin zaman ve enerjinin aynı anda ve doğru olarak saptanamayacağı anlamına geldiğini fakat bunun bir deney ile geçersizliğinin gösterilebileceğini açıklıyordu. Bunu dinleyen Bohr, uykusuz bir geceden sonra Einstein’ın düşünüşündeki hataları bularak “belirsizlik ilkesinin” yaygın olarak kabulünü sağlıyordu.
Niels Bohr ile tartışmaları
Fotoelektrik olayını açıklayan Einstein kuantum kuramının gelişimine büyük katkıda bulunmuştu ama kuramın geliştiği yönden hiç memnun değildi. Heisenberg’in belirlenemezlik ilkesini kabul etmiyor, Tanrı zar atmaz diyordu. Niels Bohr da kuantum kuramının gelişmesinde önemli rol oynamış fizikçilerden birisiydi ve Einstein’ın bu fikirlerine katılmıyordu. Einstein ve Bohr arasında birbirine saygılı bir biçimde, dostça bir tartışma sürdü. Einstein çeşitli düşünce deneyleri ile kuantum kuramının belirlenemezlik ilkesini çürütmeye çalışıyordu fakat Bohr bu eleştirilere tutarlı cevaplar vererek Einstein’ı ve dünyayı ikna ediyordu.[35] Einstein sonradan belirsizlik ilkesini çürütmeye çalışmaktan vazgeçmiş ve kuantum mekaniğinin fiziksel gerçekliği anlatmakta yetersizliği fikrini savunmaya başlamıştır.[35]
1927 yılında Solvay Konferansında Einstein ile Bohr arasında geçen o sıcak tartışmaların özünde temel kuram ve yasalar bulma saplantısı, yani son bilgi saplantısı yatıyordu. Bu çaba mutlak olanı bulma çabasıydı.[36]
Kozmoloji
Einstein evrenin sabit olduğunu düşünüyordu ve parametreler arasındaki çelişkiyi çözmek için kuramına kozmolojik sabit eklemişti.[37] Einstein sonradan belirsizlik ilkesini çürütmeye çalışmaktan vazgeçmiş ve kuantum mekaniğinin fiziksel gerçekliği anlatmakta yetersizliği fikrini savunmaya başlamıştır.[35] Sonrasında evrenin sürekli genişlediği anlaşılınca Einstein bu sabiti “en büyük hatam” olarak nitelemiş ve denklemlerinden çıkarmıştır.
Birleşik alan kuramı
Einstein, Princeton’da fizik çalışmalarını sürdürürken, genel göreliliği elektromanyetik kuramına bağlayan bir birleşik alan kuramı üzerinde çalışmış ama başarılı olamamıştır.
Görüşleri
Politik görüşleri
Einstein Almanya’da doğmuş bir Yahudi olarak Nazilerin yükselişi, iktidarı ve Holokost döneminde yaşamıştı. Bu nedenle ABD’ye göç etmiş ve büyük bir Nazi karşıtı görüş geliştirmiştir. Bilim adamlarına Nazi baskısının artması üzerine 1933 yılında Atatürk’e mektup[38] yazarak Türkiye’ye kabul edilmelerini istemiştir; bunun sonucunda gelen yüzlerce Yahudi bilim insanı Türk üniversitelerine büyük katkı sağlamıştır. Yine ABD başkanına mektup yazarak ABD’nin Almanya’dan önce nükleer silah geliştirmesi gerektiği tavsiyesinde bulunmuştur. Yahudilerin kendi ülkelerine sahip olması gerektiğine inanmış ve İsrail’in kuruluşunu desteklemiştir.[39] Ama bu devletin sınırları ve bir ordusu olmasına karşı çıkmış ve Araplar ile birlikte iki uluslu bir ülke olması gerektiğini savunmuştur.[39]
Einstein, sosyalizm hakkında övgü dolu sözler söylemiş ve bütün dünyanın tek bir hükûmet altında toplanması fikrini ifade etmiştir. Soğuk Savaş’ın başlaması ile ABD’deki anti-komünist politikalarını ifade özgürlüğünü kısıtlayacak derecede olmaları nedeniyle eleştirmiştir. Kendisi ayrıca Bertrand Russell ile birlikte bir anti-nükleer manifesto yayımlamıştır.
Niçin Sosyalizm yazısında kapitalizmi şu şekilde eleştirmiş ve sosyalizmi savunmuştur.
| “ | Bana kalırsa kapitalizmin en büyük kötülüğü bireylerin sakatlanmasıdır. Tüm eğitim sistemimiz bu beladan muzdariptir. Gelecekteki kariyerine hazırlanmak için açgözlü bir biçimde başarıya tapmak üzere eğitilmiş öğrenciye abartılı bir rekabetçi yaklaşım aşılanır. Ben bu korkunç beladan kurtulmanın tek yolu olduğuna eminim. Bu yol, toplumsal hedefler doğrultusunda yönlendirilmiş bir eğitim sisteminin eşlik ettiği sosyalist ekonominin inşasıdır. Böyle bir ekonomide toplumun kendi üretim araçlarının sahibidir ve üretim araçları planlı bir tarzda kullanılır. Üretimi toplumun gereksinimlerine uyduran planlı bir ekonomi işi çalışabilir durumda olanlara dağıtır ve erkek, kadın, çocuk herkesin geçimini garanti eder. Bireyin eğitimi, doğuştan sahip olduğu yeteneklerin geliştirilmesinin yanında, günümüz toplumundaki güç ve başarının yüceltilmesi yerine, bireyin içinde çevresindekilere karşı sorumluluk hissi geliştirmeyi hedefler.[40] | „ |
Dini görüşleri
Einstein çeşitli röportajlarında ve mektuplarında hiçbir dine inanmadığını ve bütün dinleri çocukça batıl inançlar olarak gördüğünü söylemiştir.[41] Fakat kendini bir ateist ya da panteist olarak tanımlamayıp değişik zaman dilimlerinde agnostik veya deist[42] görüşler belirtmiştir. Katı bir determinizme inanan Einstein, evrenin yasalarını anlamayı bir tür dini duyguya benzetmiştir. Ancak kendinin dini fikirleri konusunda tartışmalar hâlen devam etmektedir.
Kendisi bir kitabında dini şu şekilde tanımlamıştır:
| “ | Gerçeğin ve onun insan aklına eşsiz biçimde erişebilmesinin mantıklı yapısına duyulan bu inancı “din” kelimesinden daha iyi ifade edecek bir şey bulamadım. Bu inancın olmadığı yerde bilim, yavan bir süreç haline gelir. Eğer rahipler bunu kendi çıkarları için kullanacaklarlarsa bırakalım da bunu şeytan düşünsün. Bunun için herhangi bir ilaç yoktur.[43] | „ |
Albert Einstein, kendi Tanrı görüşünü de şu şekilde dile getirmiştir:
| “ | Daha yüksek bir düzenin bütün bilimsel çalışmasının arkasında dünyanın mantıklı veya anlaşılabilir şekilde yaratılmış olduğuna dair, dini duyguya benzer, bir inanç olduğu kesindir… Kendisini deneyim dünyasında ortaya koyan üstün bir akıl içerisinde yer alan bu sağlam, derin duygulara sıkı sıkıya bağlı inanç benim Tanrı anlayışımı anlatmaktadır.[44] | „ |
50. yaş gününde, George Sylvester Viereck’e verdiği bir röportajda Tanrı ve din ile ilgili fikirlerini şu şekilde özetlemiştir:[45]
| “ | Ben bir ateist değilim ve kendime bir panteist de diyebileceğimi düşünmüyorum. İlgili soru bizim kısıtlı akıllarımız için çok geniş. Biz, pek çok değişik dilde kitapla doldurulmuş bir kütüphaneye giren küçük bir çocuğun durumundayız. Çocuk kütüphanedeki kitapları birisinin yazmış olması gerektiğini bilir. Nasıl yazıldıklarını bilmez. Yazıldıkları dilleri anlamaz. Çocuk, kitapların sıralanmasında esrarengiz bir düzen olduğundan şüphe eder, ama ne olduğunu bilmez. Bu durum, bana göre, en zeki insanın bile Tanrı’ya göstereceği yaklaşımdır. Biz, evrenin muhteşem bir şekilde düzenlendiğini ve belirli kanunlara uyduğunu görmekteyiz, ancak bu kanunları çok bulanık bir şekilde anlayabilmekteyiz.[45] | „ |
Popüler kültürde Einstein
Albert Einstein, pek çok popüler kültür ürünü için konu veya bir ilham kaynağı olmuştur.
Einstein’ın 72. yaş gününde, UPI fotoğrafçısı Arthurr Sasse kendini kameraya karşı gülümsetmeye çalışıyordu. Einstein o gün defalarca kameralara gülümsedikten sonra bu sefer dilini çıkardı. Bu fotoğraf Einstein’ın en ünlü fotoğraflarından biri olmuştur. 19 Haziran 2009’da orijinal fotoğraf bir açık arttırmada 74,324 dolara satılmış ve Einstein’ın en pahalı fotoğrafı olmuştur.
1999’da, Einstein’ın ileri gelen fizikçiler tarafından tarihin en büyük fizikçisi seçilmesinin de etkisiyle, Einstein kelimesi, dâhileri tanımlamak için kullanılan bir kelimeye de dönüşmüştür.
Einstein ayrıca kurgu eserlerde çılgın bilim insanı tipleri için de bir model olmuştur. Aşırı ifadeli suratı ve farklı saç modeli çoğunlukla taklit edilmiş ve abartılmıştır. Time Dergisinin yazarı Frederic Golden’a göre Einstein “bir çizgi romancının gerçeğe dönüşmüş hayaliydi”.
31 Aralık 1999’daki ayrı bir sayıda Time, Albert Einstein’ı “Yüzyılın Kişisi” olarak seçmiştir.
Eserleri
Bu liste tam bir liste değildir ve göreceli olarak önemli eserlerini içermektedir.
|
Vikipedi’nin kardeş projelerinden
Albert Einstein hakkında daha fazla bilgi edinin |
|
| Commons’ta dosyalar | |
| Vikisöz’de alıntılar | |
| Vikikaynak’ta belgeler | |
Kitapları
- Görelilik; Özel ve Genel Kuram: Popüler Bir Yorum, 1920.
- Görelilik’in Anlamı, 1921.
- Tek Atomlu İdeal Gazların Kuantum Kuramı, 1924.
- Brown Hareketi Kuramı Üzerine Araştırmalar, 1926.
- Siyonizm Hakkında, 1930.
- Niçin Savaş, 1933.
- Gördüğüm Kadarıyla Dünya, Denemeler, 1934.
- Felsefem, 1934.
- Fiziğin Evrimi, Leopold Infield ile birlikte, 1938.
- Otobiyografik Notlar, Denemeler, 1949.
- Denemeler, 1950.
Makaleleri
- Über Einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (Işığın Oluşumu ve Dönüşümü Üzerine Bir Görüş), 1905.
- Über die von der molekularkinetichen Theorie der Wärme geoforderte Bewegung von ruhenden Flüssigkeiten suspendierten Teilchen (Durağan Bir Sıvı İçindeki Asıltı Parçacıklarının Moleküler Kinetik Kuramı Çerçevesindeki Hareketleri Üzerine), 1905.
- Zur Elektrodynamik bewegter Körper (Hareketli Cisimlerin Elektrodinamiği), 1905.
- Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? (Bir Cismin Eylemsizliği Enerji içeriğine Bağlı mıdır?), 1905.
- Zur Theorie der Brownischen Bewegung (Brown Hareketi Kuramı Üzerine), 1906.
- Zur Theorie der Lichterzeugung und Lichtabsorption (Işığın Salınımı ve Soğurumu Kuramı Üzerine), 1906.
- Plancksche Theorie der Strahlung und die Theorie der Spezifischen Wärme (Işınımın Planck Kuramı ve Özgül Isı Kuramı), 1907.
- Entwurf einer verallegemeinerten Relativitätstheorie und einer Theorie der Gravitation (Bir Kütle Çekimi Kuramı ve Genelleştirilmiş Görelilik Kuramına Bir Gönderme), 1913.
- Die Grundlagen der allgemeinen Relativitätstheorie (Genel Görelilik Kuramı’nın Temelleri), 1916.
- Quantentheorie der Strahlung. (Kuantum Kuramı), 1917
Genel görelilik

Genel görelilik teorisi (kısaca genel görelilik), 1915’te Albert Einstein tarafından yayımlanan, kütleçekimin geometrik teorisidir ve modern fizikte kütle çekiminin güncel açıklamasıdır.[1] Genel görelilik, özel göreliliği ve Newton’ın evrensel çekim yasasını genelleştirerek, yerçekimin uzay ve zamanın veya dört boyutlu uzayzamanın geometrik bir özelliği olarak birleşik bir tanımını sağlar. Özellikle uzayzaman eğriliğine maruz kalmış maddenin ve radyasyonun, enerjisi ve momentumuyla doğrudan ilişkilidir. Bu ilişki, kısmi bir diferansiyel denklemler sistemi olan Einstein alan denklemleriyle belirlenir.
Genel göreliliğin zamanın akışı, uzayın geometrisi, serbest düşme yapan cisimlerin hareketi, ışığın yayılımı gibi konulardaki öngörüleri, klasik fiziğin önermeleri ile belirgin farklılıklar gösterir. Kütleçekimsel zaman genişlemesi, kütleçekimsel merceklenme, ışığın kütleçekimsel kızıla kayması, kütleçekimsel zaman gecikmesi bu farklılıkların örnekleridir. Genel göreliliğin bugüne kadarki tüm önermeleri deney ve gözlemler ile doğrulanmıştır. Her ne kadar genel görelilik kütleçekimin tek göreli kuramı olmasa da, deneysel veri ile uyum sağlayan en basit teoridir. Buna rağmen, teorinin hala cevaplayamadığı sorular varlığını sürdürmektedir. Bunlara örnek olarak pioneer anomalisi, galaksilerin dönüş eğrisi ve genel görelilik ile kuantum mekaniğinin yasalarının hangi şekilde bağdaştırılarak, tamamlanmış kendi içinde tutarlı bir kuantum alan kuramı yaratılabileceğidir.
Einstein’ın teorisinin astrofiziğe kayda değer etkileri olmuştur; örneğin, büyük bir yıldızın ömrünün sonuna yaklaştığı bir zamanda içine çökerek karadelik oluşturduğuna işaret eder. Bazı astronomik cisimlerin yaydığı yoğun radyasyona karadeliklerin sebep olduğuna dair yeterli kanıt mevcuttur. Örneğin mikrokuasarlar, yıldız kaynaklı kara delikler ve etkin galaksi çekirdekleri, süper kütleli kara deliklerin varlıklarının bir sonucu olarak oluşurlar. Işığın kütleçekim nedeniyle bükülmesi, uzaktaki bir astronomik cismin gökyüzünde aynı anda birden fazla yerde görüntüsünün belirmesine sebep olan, kütleçekimsel merceklenme olarak adlandırılan bir duruma neden olur. Genel görelilik aynı zamanda, bugüne kadar ancak dolaylı olarak gözlenmiş olan, kütleçekim dalgalarının da varlığını öngörmektedir. Buna dair doğrudan gözlemlerin yapılması LIGO ve NASA/ESA Laser Interferometer Space Antenna (Lazer girişimölçer uzay anteni) gibi projelerin amaçlarıdır. Tüm bunlara ek olarak genel görelilik, evrenin durmaksızın genişleyen modelinin bugünkü kozmolojik modelinin temelidir.
Tarihi
1905’te özel görelilik teorisini açıkladıktan hemen sonra, Einstein bu göreli çerçeveye kütleçekimini nasıl dahil edeceğine dair fikir yürütmeye başladı. 1907 yılında serbest düşen bir gözlemciyi ele alan basit bir düşünce deneyinden yola çıkarak, kütleçekimin göreli teorisi üzerine sekiz yıl sürecek bir araştırmaya başladı. Birçok denemenin ardından, bugün Einstein alan denklemleri olarak bilinen çalışmasını sonlandırarak, Kasım 1915’te Prusya Bilimler Akademisi’nde sundu. Bu denklemler Einstein’ın kuramının çekirdeğini oluşturur ve herhangi bir maddenin uzay ve zamanı nasıl etkilediğini belirler.[2]
Einstein alan denklemleri doğrusal olmayan ve çözümü oldukça zor olan diferansiyel denklemlerdir. Einstein, başlangıçta kuramını öngörüye dayanarak biçimlendirmişti. Ancak çok zaman geçmeden 1916 yılında, astrofizikçi Karl Schwarzschild Einstein alan denklemlerinin ilk kesin ve sıfırdan farklı çözümünü bulmayı başardı. Bu çözüm Schwarzschild metriği olarak adlandırılır.
Schwarzschild metriği ile, kütleçekimsel içe çökmenin son evrelerinin, yani bugün bilinen adıyla karadeliklerin tanımının temelleri ortaya koyulmuştur. Aynı yıl Schwarzschild çözümünün elektrik yüklü cisimler için genelleştirilmiş çözümü olan Reissner – Nordström çözümüne ulaşıldı. Bugün bu çözüm elektrik yüklü karadelikler için kullanılmaktadır.[3]
1917’de Einstein, kuramını, evrenin bütününe uygular ve göreli kozmolojinin temelini atar. Genel göreliliğin öngörüsü evrenin genişlemekte ya da büzülmekte olduğu iken, Einstein evrenin durağan olduğunu düşünmüştür ve bunu sağlamak için orijinal alan denklemlerine kozmolojik sabit olarak adlandırdığı yeni bir değişken ekler.[4]
Ancak 1929’da Hubble, evrenin durağan olmadığını, uzak gökadaların tayfının kırmızıya kaydığını buldu. Friedmann 1922’de yaptığı çalışmada genişleyen evren modelini kozmolojik sabit kullanmaksızın ortaya koymuştur. Lemaître bu çözümü Büyük patlama’nın ilk modelini formüle etmek için kullanmıştır.[5] Evrenin genişlediğine dair gözlemlerden sonra Einstein, kozmolojik sabiti, “hayatının en büyük hatası” olarak tanımlar.[6]
Bu süre zarfında genel görelilik merak uyandıran bir kuram olarak kalır. Özel göreliliğin yasaları ile uyumlu olması ve Newton kuramının açıklayamadığı bazı etkilere cevap getirmesi nedeniyle açıkça Newtonsal kütleçekime karşı bir üstünlüğü vardır. 1915’te kuramının Merkür’ün günberi devinimi sorununa isteğe bağlı değişkenler kullanmadan nasıl açıklık getirdiğini, Einstein bizzat kendisi açıklamıştır.[7] 1919’da Eddington tarafından yönetilen bir keşif, 29 Mayıs 1919 tarihindeki tam güneş tutulması sırasında yıldız ışığının güneş tarafından aynı genel göreliliğin öngördüğü şekilde büküldüğünü doğrulamış[8] ve bu, Einstein’ın ününü daha da arttırmıştır.[9] Ancak kuram, altın çağını 1960 ve 1975 yılları arasında yaşamış ve ancak bundan sonra teorik fiziğin ana dallarından biri olarak kabul görmüştür.[10]
Klasik mekanikten genel göreliliğe
Genel göreliliği iyi anlamanın yolu klasik mekanik ile benzerliklerini ve farklılıklarını gözden geçirmektir. Öncelikle klasik mekaniğin ve Newton’un kütleçekim yasasının geometrik bir şekilde tanımlanabileceği bilinmelidir. Bu tanım özel göreliliğin yasaları ile birleştirilerek, genel göreliliğin yasaları becerikli bir fizikçi tarafından türetilebilir.[11]
Newton kütleçekiminin geometrisi

Klasik mekaniğin özünde, bir cismin hareketinin serbest (ya da ivmeli) hareketinin ve bu serbest hareketten sapmaların bileşimi yatar. Bu sapmalar cisme etkiyen dış kuvvetlerin varlığından kaynaklanır ve kuvvetin tanımı Newton’un ikinci yasası ile verilmiştir. İkinci yasa bir cisme etkiyen net kuvvetin cismin eylemsiz kütlesi ve ivmesinin çarpımı kadar olacağını söyler.[12] Cismin tercih edeceği eylemsiz hareket, uzay ve zamanın geometrisine bağlıdır: Standart olarak klasik mekaniğin konuşlanma sistemlerinde serbest hareket yapan cisimler düz çizgiler boyunca sabit hızla hareket ederler. Günümüz terminolojisinde, cisimlerin eğri uzayzamandaki bu yollarına jeodezik denilmektedir.[13] Aksine bir zaman koordinatının yanı sıra, gözlemleyerek ve dış kuvvetleri (elektromanyetizma ve sürtünme gibi) tolerans ederek tanımlanan eylemsiz hareketlerin uzayın geometrisini belirlemek için kullanılması beklenilebilir. Fakat yerçekimi devreye girer girmez bir belirsizlik oluşur. Newton’un evrensel kütleçekim yasası ve bağımsız doğrulanan Eötvös deneyi ve onun ardıllarına göre, serbest düşüşün bir evrenselliği vardır. (ayrıca eylemsiz ve pasif yerçekimsel kütlenin evrensel eşitliği ya da zayıf eşdeğerlik ilkesi olarak da bilinir): serbest düşüş halindeki test cisminin yörüngesi sadece pozisyonuna ve ilk hızına bağlıdır fakat materyal özelliklerine bağlı değildir. Bunun basitleştirilmiş versiyonu Einstein’ın asansör deneyinde, sağ tarafta gösterilen figürde, somutlaştırılır. Küçük kapalı bir odadaki bir gözlemci için odanın kütleçekimsel alanda durağan ya da kütleçekimine eşit kuvvet üreten ve ivmelenen bir rokette boş uzayda olup olmadığına aşağı bırakılan bir cisim gibi yörüngelerini haritalayarak karar vermek mümkün değildir.
Serbest düşüşün evrenselliği göz önünde tutulursa eylemsiz hareket ile kütleçekimsel kuvvet etki altındaki hareket arasında gözlemlenilebilir fark yoktur. Bu kütleçekimi etkisi altında serbest düşüş yapan cisimler olarak adlandırılan eylemsiz hareketin yeni bir sınıfının tanımını destekler. Tercih edilmiş hareketlerin yeni sınıfı ayrıca matematik terimleri ile uzayın ve zamanın geometrisini açıklar.Bu bir kütleçekimsel potansiyelin değişim derecesine bağlı olan özel bağlantı ile ilişkili jeodezik bir harekettir. Bu yapıdaki uzay hala tipik bir Öklit geometrisine sahiptir. Fakat uzay zaman bir bütün olarak daha karışıktır. Farklı test parçacıklarının serbest düşüş yörüngelerini takip eden basit bir düşünce deneyi kullanarak gösterilebileceği üzere, bir parçacığın hızını gösterebilen uzay zaman vektörlerinin (zaman vektörleri gibi) taşınmasının sonucu parçacığın yörüngesine göre değişiklik gösterecektir; matematiksel konuşmak gerekirse Newtonsal ilişkisi tümlevlenemez. Bundan uzay zamanın eğri olduğu sonucu çıkarılabilir. Sonuç sadece eşdeğişken (kovaryant) kavramları kullanan Newton kütleçekiminin geometrik bir denklemlendirilmesidir, yani herhangi bir koordinat sisteminde geçerli olan bir tanımdır. Bu geometrik tanımda gelgit etkileri (serbest düşüş halindeki cisimlerin göreceli ivmesi) kütlenin varlığının geometriyi nasıl değiştirdiğini gösteren bağlantının türevi ile ilişkilidir.
Göreli Genelleme
Geometrik Newton yerçekimi ne kadar ilgi çekici olsa da temeli olan klasik mekanik, sadece (özel) göreli mekaniğin sınırlayıcı bir durumudur. Kütleçekiminin ihmal edilebileceği simetri dilinde klasik mekanikteki fizik Galile değişmezliği yerine genel görelilikte olduğu gibi Lorentz sabitidir. (Genel göreliliği tanımlayan simetri ayrıca öteleme ve dönmeyi içeren Poincaré grubudur). İkisi arasındaki farklılık ışık hızına yaklaşan hızlarda ve yüksek-enerji durumlarında uğraştığımızda daha fazla öneme sahip olur.
Lorentz simetrisi ile ilave yapılar devreye girer. Bunlar ışık konileri grubu (sol taraftaki resim) ile tanımlanırlar. Işık konileri nedensel bir yapı oluştururlar: her A olayı için prensipte ya etkileyen ya da sinyal yolu ile ya da ışıktan fazla hızlı yol almasına gerek olmayan etkileşimlerden (resimdeki B olayında olduğu gibi) etkilenen olaylar topluluğu vardır ve böyle bir etki için olaylar topluluğu mümkün değildir. (resimdeki C olayında olduğu gibi) Bu gruplar gözlemciden bağımsızdır. Serbest düşüş yapan parçacıkların hayat çizgisi ile bağlantılı olarak ışık konileri uzay zamanın yarı Riemannian metriğini tekrar oluşturması için kullanılabilir, en azından pozitif bir sayısal faktöre bağlı olarak. Matematik terimlerinde bir konform yapıyı tanımlar.
Özel görelilik kütleçekimi yokluğunda tanımlanır. Bu yüzden pratik uygulamalar için ne zaman kütleçekimi ihmal edilebilirse edilsin bu uygun bir modeldir. Eğer yerçekimini dahil eder ve serbest düşüsün evrenselliğini varsayarsak bir önceki bölümdeki benzer bir düşünce uygulanır: evrensel eylemsiz çerçeveler yoktur. Bunun yerine serbest düşüş yapan parçacıkların yanı sıra hareket eden yaklaşık olarak eylemsiz çerçeveler vardır. Uzay-zaman diline çevrilirse, kütleçekimi serbest bir eylemsiz çerçevesi tanımlayan düz zaman çizgileri birbirine göre eğilmiş çizgilere dönüşür (kütleçekiminin dahil edilmesinin uzay zaman geometrisinde bir değişiklik gerektirdiğini farz edersek).
Serbest düşüşteki yeni kısmi çerçevelerin özel görelilik yasalarının (teori ışığın yayılımına dayalıdır ve bu yüzden elektromanyetizmaya da bağlıdır) uygulandığı referans çerçeveleri ile uyuşup uyuşmadığı açık değil. Fakat özel göreli çerçeveler hakkında farklı varsayımlar kullanarak (dünyada sabit olmaları ya da serbest düşüşte olmaları gibi) kütleçekimsel kırmızıya kayma tahminleri türetilebilir. Kütleçekiminden dolayı kırmızıya kayma ışığın yerçekimsel bir alana doğru yayılırken frekansının değişmesidir. Gerçek ölçümler serbest düşüş çerçevelerinde ışığın özel görelilikte olduğu gibi yayıldığını gösterir. Serbest düşüş (ve dönmeyen) çerçeve referanslarındaki özel görelilik yasası ile adlandırılan durumun genelleştirilmesi Einstein’in eşitlik ilkesi olarak bilinir. (özel-göreli fiziği kütleçekimini içerecek şekilde genelleştirmek için çok önemli yol gösterici bir ilkedir.)
Aynı deneysel bilgiler yerçekimsel bir alanda saatlerle ölçülen zaman özel görelilik kurallarını takip etmez. Uzay zaman geometrisi dilinde Minkowski metriği ile ölçülmez. Newtonsal durumda olduğu gibi bu daha fazla genel bir geometriyi akıla getirir. Küçük ölçeklerde serbest düşüşteki bütün çerçeve referansları eşittir ve yaklaşık olarak Minkowakiandır. Bu yüzden Minkowski uzayının eğri bir genelleştirilmesi ile uğraşmıyoruz. Geometriyi özellikle açıların ve uzunlukların nasıl ölçüldüğünü tanımlayan metrik tensörü özel göreliliğin Minkowski metriği değildir. Yarı-Riemann metriği olarak bilinen bir genellemedir. Hatta her Reimannian metriği doğal olarak özel bir bağlantı türü ile ilişkilidir, Levi-Civita bağlantısı ve aslında eşitlik ilkesini karşılayan ve uzayı Minkowskian yapan bir bağlantıdır. (uygun yerel bir eylemsiz koordinatlarda metrik Minkowskiandır ve kısmi türevleri ve bağlantı katsayıları sıfır olur.)
Einstein’in Denklemleri
Kütleçekiminin göreli geometrik versiyonunun etkilerini formülleştirdikten sonra yerçekiminin kaynağı sorusu geride kalır. Newton yerçekiminde kaynağı kütledir. Özel görelilikte kütle stresin(basınç ve kayma) yanı sıra enerji ve moment yoğunlukları içeren enerji-momentum tensör olarak adrandırılan daha genel bir niteliği çağrıştırır. Eşitlik ilkesini kullanarak bu tensör kolayca eğri uzay zamana genelleştirilir. Analojiyi geometrik Newton yerçekimi ile kaleme alırsak yerçekimi için alan denkleminin bu tensör ve özel bir gelgit etkilerinin sınıfını tanımlayan Ricci tensörü ile ilgili olduğunu varsaymak doğaldır (ilk başta durağan ve sonra serbest düşüş yapan küçük bir test parçacıkları grubu için hacimdeki değişim). Özel görelilikte enerjinin korunumu (momentum, enerji durumuna karşılık gelir) momentum tensörü ıraksayışı serbesttir. Bu formül ayrıca kısmi türevleri diferansiyel geometride çalışılan eşdeğişkin türevleri olan eğri-manifold karşılıkları ile değiştirerek kolayca eğri uzaya genelleştirilebilir. Bu ek koşul ile enerji-moment tensörünün eğdeğişken ıraksayışı ve bu nedenle denklemin diğer tarafında ne olursa olsun Einstein’in (alan) denklemleri olarak adlandırılan en basit bir takım denklemler:
-
Einstein’in alan denklemleriGμν≡Rμν−12Rgμν=8πGc4Tμν
Sol taraftaki Einstein tensörüdür, Ricci tensörünün Rμν özel ıraksayışı serbest kombinasyonu ve metriğidir. Gμν simetriktir. Özellikle,
- R=gμνRμν
eğrilik skalerdir. Ricci tensörü daha genel Riemann eğrilik tensörü ile ilgilidir.
- Rμν=Rαμαν.
Sağ taraftaki, Tμν enerji-moment tensörüdür. Bütün tensörler soyut dizin semboller ile yazılır. Gezegen yörüngeleri için teorinin tahminleriyle gözlemlenen sonuçları eşleştirirsek orantı sabiti 8πGc4 olarak sabitlenebilir, G kütle çekimi sabiti ve c ışığın hızıdır. Enerji-momentum tensörünün ortadan kalkması için madde mevcut olmadığında, sonuçlar vakum Einstein denklemleridir,
- Rμν=0.
Tanım ve temel uygulamalar
Bir önceki bölümde bahsedilen türev, inşa modeli için nasıl bir teori kullanılabileceğini açıklayan, fizikteki önemli bir sorunun adresi ve anahtar özelliklerini tanımlayan, genel göreliliği tanımlayabilmek için gerek duyulan bütün bilgileri içerir.
Tanım ve temel özellikler
Genel görelilik yerçekiminin bir metrik teorisidir. Dört boyutlu bir geometri, uzay zamanı belirten pseduo-Reimannian ile uzay zamanda bulunan enerji-moment arasındaki ilişkiyi tanımlayan Einstein’in denklemleri bir çekirdek gibidir. Kütleçekimi kuvveti (serbest düşüş, orbital hareket ve uzay aracı yörüngeleri gibi) etkisini isnat eden klasik mekanikteki olay, genel görelilikteki uzay zamanın eğik geometrisindeki eylemsiz harekete denk gelir. (nesneleri düz ve doğal yollarından saptıran bir kütleçekimi kuvveti yoktur.) Aslında kütleçekimi uzay ve zamandaki değişikliklerine karşılık gelir- nesnenin doğal bir biçimde takip edebileceği mümkün en düz yolları değiştirir. O halde eğiklik maddenin enerji- momentumundan dolayı oluşur. John rölativist Archibald Wheeler’ e göre uzay zaman maddeye nasıl hareket edeceğini söyler, madde uzaya nasıl bükeceğini söyler.
Genel görelilik, klasik fiziğin skaler kütleçekimi potansiyelini simetrik bir iki-kademeli tensör ile değiştirirken, ikincisi bazı sınırlayıcı durumlarda birincisine indirgenir. zayıf kütleçekimi alanları ve ışığın hızına göre yavaş hız için teorinin tahminleri Newton’un evrensel kütleçekimi yasasını birleştirir.
Tensörleri kullanarak oluşturulduğu üzere, genel görelilik genel kovaryansı gösterir. Yasaları (ve genel göreli çerçeve içinde formüle edilen diğer yasalar) tüm koordinat sistemlerinde aynı biçimi alır. Ayrıca, teori herhangi bir değişmez geometrik arka plan yapısı içermez, yani arka plandan bağımsızdır. Böylece göreliliğin daha katı bir genel ilkesini, yani fizik yasalarının tüm gözlemciler için aynı olduğu ilkesini karşılar. Yerel olarak, eşdeğerlik ilkesinde ifade edildiği gibi, uzay-zaman Minkowskiyen’dir ve fizik yasaları yerel Lorentz değişmezliği sergiler.
Model oluşturma
Genel göreli model oluşturmanın ana fikri Einstein’in denklemlerinin bir çözümünden gelir. Einstein’in denklemleri ve maddenin özellikleri için uygun denklemlere göre böyle bir çözüm spesifik bie yarı-Riemmannian kopyası (genellikle spesifik koordinatlarda metrik vererek tanımlanan) ve spesifik o kopyada tanımlanan madde alanlarından oluşur. Madde ve enerji Einstein’in denklemlerini sağlamalıdır, bu yüzden özellikle maddenin enerji-moment tensörü ıraksaması sabit olmalıdır. Tabii ki madde ayrıca herhangi ek denklemleri de sağlamalıdır. Kısacası, böyle bir çözüm genel göreliliğin yasalarını tatmin eden bir modeldir ve mümkün olduğunca herhangi maddeyi ele alan ilave yasalar ortaya konulabilir.
Einstein’in denklemleri doğrusal olmayan kısmi diferansiyel denklemlerdir ve çözümü de zordur. Yine de, sadece birkaçı direkt fiziksel uygulamalara sahip olsa da, birkaç tamı tamına doğru çözümleri vardır. Bilinen en iyi tam çözümleri ve ayrıca fizik görüşü açısından en ilgi çekici olanları Schwarzschild çözümü, Reissner-Nordström çözümü ve Kerr metriği (başka bir boş uzayda her biri kara cismin belirlenmiş bir türüne karşılık gelir) ve Friedmann – Lemaître – Robertson – Walker ve de Sitter evrenleridir (her biri genişleten bir kozmosu tanımlar). Büyük teorik görüşünün tamı tamına çözümleri Gödel evrenini (eğri uzay zamanlarda, zaman yolculuğunun merak uyandırıcı bir olasılığına açık), Taub-NUT çözümü (homojen fakat eşyönsüz bir evren) ve anti-de Sitter uzayını (son zamanlarda Maldacena ikiliği ile ön planda olan) içerir.
Tam çözümleri bulmadaki zorluk durumunda bilgisayarda integral ile ya da asıl çözümlerin küçük sapmalarını düşünerek Einstein’in alan denklemleri ayrıca sık sık çözülür. Numarasal göreli alanlarda, iki çarpışan kara delik gibi Einstein’in ilginç durumlarda denklemlerini çözmek için ve uzay zaman geometrisini benzeştirmek için güçlü bilgisayarlar kullanılır. Özellikle yeterli bilgisayar kaynakları ile bu metotlar herhangi bir sisteme uygulanabilir ve yalın tuhaflıklar gibi temel problemlere çözüm kazandırabilir. Doğrusallaşmış kütleçekimi ve genelleştirilmesi, post-Newton genişlemesi, gibi sapma teorileri ile yaklaşık sonuçlar bulunabilir. Işığa kıyasla yavaşça hareket eden bir madde dağılımı içeren uzay zamanın geometrisi için çözümde ikincisi sistematik bir yaklaşım sağlar. Genişleme terimlerin bir serisini içerir; ikinci terimler genel görelilik yüzünden Newton’un teorisine daha az düzeltmeleri gösterirken, birinci terimler Newton yerçekimini gösterir. Bu genişlemenin büyümesi alternatif teoriler ile genel göreliliğin tahminleri arasında nicel kıyaslamalara olanak sağlayan parametre edilmiş post-Newton’ dur.
Einstein’in teorisinin sonuçları
Genel görelilik birçok fiziksel sonuçlara sahiptir. Bazıları direkt teorinin aksiyomlarından takip eder, bazıları ise sadece Einstein’in ilk yayını olan 90 yıllık araştırmaları ile açıklığa kavuşur.
Kütleçekimsel zaman genişleşmesi ve frekans kayması
Eşdeğerlik ilkesinin geçerli olduğunu varsayarsak, zamanın akışını kütleçekimi etkiler. Kütleçekimi haznesine gönderilen ışık maviye kayar ve diğer yönden gönderilen(kütleçekimi haznesinden çıkan) ışık kızıla kayar; bu iki etkiler kütleçekimi ile frekans kayması olarak adlandırılır. Daha genel olarak, uzakta olan yerler ile karşılaştırıldığında büyük bir cismin yanında işlem daha yavaş gerçekleşir; bu etki kütleçekimsel zaman genişlemesi olarak bilinir.
Kütleçekimsel kırmızıya kayma laboratuvarda ve astronomik gözlemlerle ölçülmüştür. Küresel Konumlama Sistemi operasyonunun bir yan etkisi karşıladığı halde, dünyanın kütleçekimi alanındaki kütleçekimsel zaman genleşmesi atomik saatler kullanılarak ölçülmektedir. Bütün sonuçlar genel görelilik ile uyuşmaktadır. Fakat doğruluğun geçerli seviyesinde bu gözlemler eşiklik ilkesinin geçerli olduğu genel görelilik ve diğer teoriler arasındaki farkı ayırmaz.
Işık sapması ve kütleçekimsel zaman gecikmesi
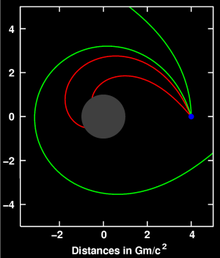
Genel görelilik, ışığın yolunun bir yıldızın yakınından geçerken uzay-zamanın eğriliğini izleyeceğini öngörür. Bu etki, yıldızların veya uzak kuasarların ışığının Güneş’ten geçerken saptığının gözlemlenmesiyle doğrulandı.
Bu ve ilgili tahminler, ışığın ışık benzeri veya boş jeodezik olarak adlandırılan şeyi takip ettiği gerçeğinden kaynaklanmaktadır (klasik fizikteki ışığın hareketine doğru olan düzgün çizgilerin bir genelleştirilmesi). Bu tür jeodezikler özel görelilikteki ışık hızı sabitinin genelleştirilmeleridir. Uygun uzay zaman modelleri (ya dış Schwarzschild çözümü ya da tek bir kütleden fazlası için Newton-sonrası açılımlar) açıklandığı üzere, yerçekiminin ışığın ortaya dağılmasındaki birçok etkileri. Serbest düşüşün evrenselliğini ışığa vererek ışığın bükülmesi türetebildiği halde, bu tür hesaplamalardan sonuçlanan ışının sapması sadece genel görelilik tarafından verilen değerin yarısıdır.
Kütleçekimsel zaman gecikmesi ışığın sapması ile yakından ilgili olduğu için kütleçekimsel bir alana doğru ışık sinyallerinin hareket etmesi alan yokluğundakilere göre daha uzun sürer.bu tahmin için çok fazla başarılı testler yapılmaktadır. parametre edilmiş post-Newtoncu biçimcilikte ışığın sapmasının ve kütleçekimsel zaman gecikmesinin ölçümleri kütleçekiminin uzayın geometrisi üzerindeki etkisini şifreleyen γ ile adlandırılan bir parametreyi belirler.
Yörüngesel etkiler ve göreliliğin yönü

Temel metin: Genel görelilikte Kepler sorunu
Yörüngesel cisimler konusundaki birçok tahminler açısından genel görelilik klasik mekanikten farklıdır. Gezegensel yörüngelerin tam bir dönüşünü tahmin eder. (kütleçekimsel dalgaların emilimi ve göreliliğin yönü ile ilgili etkilerin neden olduğu yörüngesel gecikmelerde olduğu gibi)
Apsislerin devinimi

Genel görelilikte herhangi bir yörüngenin apsisi (yörüngesel hareket eden bir cismin sistemin kütlesinin merkezine en yakın olduğu yer) devinecektir- yörünge eliptik değildir fakat odağına göre dönen bir elipse benzer(gül eğimi gibi bir şekil ile sonuçlanır (resmi gör)). Einstein ilk olarak yörüngesinde hareket eden bir cisme bir test parçacığı gibi davranarak ve Newton limitini gösteren yaklaşık bir metrik kullanarak bu sonucu çıkardı. Urbain Le Verrier tarafından 1859’da keşfedilen Merkür gezegeninin anormal günberi değişiminin açık bir açıklamasını veren teorisi onun için kütleçekimsel alan denklemlerinin doğru halini tanımladığı önemli bir kanıttı. Tam tamına Schwarzschild metriği (uzay zamanı küresel bir kütle etrafında tanımlayan) ya da daha gele post-Newton biçimciliği kullanarak etki ayrıca türetebilir. Bu durum, bir cismin kütleçekiminin öz enerjine katkısı (Einstein’in denklemlerinin doğrusal olmayışlığında şifrelenen) ve kütleçekiminin uzayın geometrisindeki etkisinden dolayıdır. Kesin devinim ölçümleri sağlayan bütün gezegenler (Merkür, Venüs ve Dünya) için göreli devinim gözlenmektedir.
Yörüngesel gecikme

Yörünge gecikmesi Genel göreliliğe göre, ikili sistem enerji kaybederken yerçekimsel dalgaları emecektir. Bu kayıp yüzünden iki yörüngesini izleyen iki cisim arasındaki mesafe azalır ve bu yüzden yörüngesel periyotları da azalır. Güneş sisteminde ya da sıradan çift yıldızlar için etki çok az gözlemlenebilir. İki yörüngesel hareket yapan nötron yıldızları (birisi pulsardır) yakın bir çift pulsar için değildir; pulsardan Dünyadaki gözlemciler, yörüngesel periyodun ölçümlerini sağlayan ve yüksek doğruluğa sahip saat gibi görev yapabilen düzenli bir radyo bakliyatlarını alabilirler. Nötron yıldızları çok yoğun olduğu için enerjinin önemli bir miktarı kütleçekimsel radyasyon olarak salınır.
Yerçekimsel dalgaların salınması yüzünden yörüngesel periyotlarındaki azalmanın ilk gözlemi 1974’te keşfedilen PSR1913+16 çift pulsarı kullanarak Hulse ve Taylor tarafından yapıldı. 1993 Nobel Ödülünü kazandıkları yerçekimsel dalgaların ortaya çıkımı bir ilkti. O zamandan beri birçok diğer pulsarlar bulundu; özellikle PSR J07337-3039 çift pulsarı.
Jeodezik devinim ve çerçeve sürüklenmesi
Birçok göreli etkiler yönün göreliliği ile direkt bağlantılıdır. Biri jeozdezik devinimdir: eğik uzay zamanda serbest düşüşteki bir jiroskobun yönünün ekseni, böyle bir jiroskop mümkün olduğunca kararlı bir biçimde bir yolu sürdürmenin yolunu gösterdiği halde uzak yıldızlardan gelen ışığın yönü ile karşılaştırıldıkça değişecektir. (paralel taşıma) Ay-Dünya sistemi için bu etki ayla ilgili lazer değişimleri yardımı ile ölçülmektedir. Daha yaygın olarak, % 0.3 den daha iyi bir hassasiyet ile Kütleçekimi B Araştırması uydusunda test kütleleri için ölçülmektedir.
Dönen bir kütlenin yanında çerçeve sürüklenmesi etkisi adında etkiler vardır. Uzak bir gözlemci kütleye yakın cisimler sürükleneceğini saptayacaktır. Bu aşırı dönen kara delikler içindir. (sıcak bir alana giren herhangi bir cisim için dönme kaçınılmazdır) Bu tür etkiler serbest düşüşte jiroskopların yönelimi üzerindeki etkileri ile tekrar test edilebilir. Az çok tartışmaya açık testler LAGEOS uyduları kullanarak yapılmaktadır. ayrıca Evrensel Mars Araştırmacısının Mars üzerine incelemesi kullanılmaktadır.
Astrofizik uygulamaları

Temel metin: Kütleçekimsel lens Kütleçekimi ile ışığın sapması astronomik olayın yeni bir sınıfının sorumludur. Eğer ağır bir cisim astronom ile uygun kütleli ve göreli mesafeli uzak hedef bir etkiler arasına yerleştirilir ise astronom hedefin birçok saptırılmış görüntülerini görecektir. Bu tür etkiler kütleçekimsel lens olarak bilinir. Görünüşe ve kütle dağılımına dayanarak iki ya da ikiden fazla görüntüleri olabilir, parlak çember Einstein’in çemberi olarak bilinir. En eski örneği 1979 yılında keşfedildi ve o zamandan beri yüz den fazla kütleçekimsel lensler gözlemlendi. Çözülebilmesi için birçok görüntüler birbirlerine yakın olsa bile etki hala ölçülebilir. (birçok mikro lens olayları gözlemlenmektedir)
Kütleçekimsel lens gözlemsel astronomide gelişmektedir. Kara deliğin varlığını ve yayılımını göstermek için kullanılır. (uzak galaksileri gözlemlemek için doğal bir teleskop sağlar ve bağımsız Hubble sabitinin tahminini elde etmeye katkıda bulunur) Lens bilgilerinin statiksel değerlendirmeleri galaksilerin yapısal evrimine değerli bir anlayış katar.
Kütleçekimsel dalga astronomisi
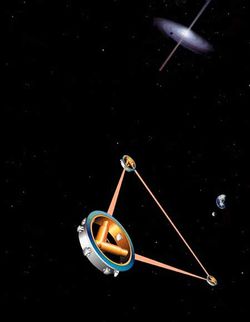
Çift pulsarların gözlemleri kütleçekimsel dalgaların varlığı için güçlü dolaylı bir kanıt sağlar. (yukarıdaki yörüngesel gecikmeyi gör) Fakat kozmosun derinliklerinden bize ulaşan kütleçekimsel dalgalar direkt olarak algılanmamıştır. Görelilikle ilgilenen araştırmacıların temel amacı böyle bir buluştur. Birçok kütleçekimsel dalga buluşları denenmektedir ve en önemlisi ferrometrik detektörlerdir: GEO 600, LIGO (iki detektör), TAMA 300 ve VIRGO . Çeşitli zamanlama okları 10−9 -10−6 Hertz frekansları aralığındaki kütleçekimsel dalgaları(çift çok ağır kara deliklerin oluşturduğu) algılamak için milisaniye pulsarları kullanır. Avrupalı uzay detektörü Elısa / NGO sürekli gelişme aşamasındadır. (başlangıcı 2015 e kadar olan haberci bir görev LISA Pathfinder ile) Kütleçekimsel dalgaların gözlemleri elektromanyetik spektrumdaki gözlemleri tamamlamaya garanti verir. Kara delikler ve nötron yıldızları, beyaz cüceler, süpernova patlamalarının türleri hakkında bilgi vermeleri beklenir.
Kara delikler ve diğer yoğun cisimler
Bir cismin kütlesinin yarıçapına oranı yeterince büyük olduğu zaman genel görelilik bir kara deliğin(hiçbir şeyin, ışığın bile kaçamadığı düşünülen) oluşumunun kaçabileceğini ileri sürer. Son zamanlarda kabul edilmiş 1.4 güneş kütleleri civarında nötron yıldızları, yıldızımsı kara delikler ve yıldız evrimi modelleri, büyük kütleli yıldızların gelişimi için final durum olduğu düşünülür. Genellikle bir galaksi merkezinde birkaç milyonluk güneş kütleye sahip bir süper kütleli kara deliğe sahiptir.
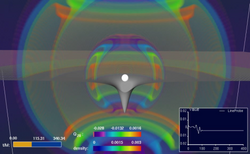
Astronomik olarak yoğun cisimlerin kütleçekimsel enerjiyi elektromanyetik radyasyona çeviren fevkalade mekaniği, onlara en önemli özelliğini katar. Gaz maddelerin ya da tozun yıldız ya da süper kütleli kara deliklere düşüşü göz alıcı bir şekilde ışıldayan bazı cisimler için sorumlu olduğu düşünülür. (oldukça galaksi ile ilgili yıldız boyutundaki cisimler(mikro yıldızımsı gökcisimleri gibi) üzerindeki aktif çekirdeğin farklı türleri) Özellikle, yığılma yaklaşık ışık hızı ile uzaya fırlatılmış yüksel enerjili parçacıkların ışınlarına odaklı göreli jetlere neden olabilir. Genel görelilik bütün bu olayları modellemede merkez bir rol oynar ve gözlemler teori ile tahmin edilen kara deliklerin varlıkları için güçlü bir kanıt sağlar. Kara delikler ayrıca kütleçekimsel dalgalar için olan araştırmalarda amaçlarında tebliğ içindedir. İkili kara deliği birleştirme Dünyadaki detektörlere ulaşan en güçlülerden bazı yerçekimsel dalga sinyallerini takip etmelidir ve birleşmeden direkt önceki safha, birleşme olaylarının mesafesini azaltmak için bir standart mum olarak kullanılabilir. Bu yüzden uzak mesafelerde kozmik genişlemenin araştırması olarak hizmet eder.
Kozmoloji

Kozmolojinin geçerli modelleri kozmoloji sabitini Λ içeren Einstein’in alan denklemelerine dayanır çünkü kozmosun büyük ölçekli dinamiğine büyük etkisi vardır.
- Rμν−12Rgμν+Λ gμν=8πGc4Tμν
gμν uzay zaman metriğidir . Bu ileri denklemlerin eş yönlü ve homojen çözümleri, Friedmann-Lemaitre-Robertson-Walker çözümleri, Büyük Patlamadan daha evvel 14 milyon yıl süreyi aşkın gelişen bir evreni modellemeye fizikçiler için olanak sağlar. Astronomik gözlemlerle birkaç parametreler(mesela evrenin madde yoğunluğu) sağlandıktan sonra ilaveten gözlemlenen veriler modelleri test etmek için kullanılabilir. Tahminler, ilkel nükleosentez, evrenin yüksek ölçekli yapısı, periyodunda oluşan ilk kimyasal elementlerin bolluğunu ve varlığını ve termal bir ekodan özelliklerini içerir. (kozmik özgeçmiş radyasyonu) Kozmolojik genişleme oranının astronomik gözlemleri, maddenin doğası gizemli kaldığı halde evrendeki toplam madde miktarının tahmin edilmesini sağlar. Bütün maddelerin yaklaşık %90 ı kara maddedir. (kütleye sahiptir fakat elektromanyetik olarak etkilemez ve bu yüzden direkt gözlemlenemez) Ana hatlarıyla bu yeni tür maddenin parçacık fiziği çatısında kabul edilmiş bir tanımı yoktur. Uzak Süpernovanın kızıla kayma incelemelerinden gözlemlenen kanıtlar ve özgeçmiş kozmik radyasyonun ölçümleri ayrıca kozmik genişlemenin ivmelenmesine ya da karanlık enerjiye neden olan kozmolojik sabitinden önemli derecede evrenin gelişiminin etkilendiğini gösterir. Yaklaşık 10−33 saniye kozmik zamanında güçlü hızlandırılmış genişlemenin enflasyon safhası adlı yeni bir faz 1980 yılında klasik kozmolojik modeller ile açıklanamayan birkaç karışık gözlemlerin yararına varsayılmıştır. Son günlerdeki kozmik özgeçmiş radyasyonunun ölçümleri bu senaryo için ilk kanıtla sonuçlandı. Fakat geçerli gözlemler ile sınırlanamayan mümkün enflasyon senaryolarının şaşırtıcı bir çeşitliliği vardır. Enflasyon safhasına öncü ve büyük patlama tuhaflığını tahmin eden klasik modellere yakın en erken evrenin fiziği daha geniş bir sorudur. Otoriter cevap henüz geliştirilmemiş olan kuantum kütleçekimi teorisine gerek vardır.
İleri kavramlar
Global geometri ve sebep gösteren yapı

Genel görelilikte bir ışığın titreşimine hiçbir şey yetişemez ya da yakalayamaz. Işık A dan X e gönderilmeden A olayından hiçbir etki diğer X yerine ulaşamaz. Neticede bütün ışık hayat çizgilerinin (geçersiz jeodezik) keşfi uzay zamanın nedensel yapısı hakkında ana bilgiler verir. Bu yapı sınırlı bir haritaya oturtmak için uzayın sonsuz geniş alanları ve sonsuz zaman aralıklarının daraltılmış olduğu Penrose-Carter diyagramlarını kullanarak gösterilebilir. (ışık hala standart uzay zaman diyagramlarında olduğu gibi köşegenlere doğru hareket eder)
Nedensel yapının öneminin farkına varan Roger Penrose ve diğerleri neyin evrensel geometri olarak bilindiğini geliştirdiler. Evrensel geometride çalışmanın amacı Einstein’in denklemlerinin belli bir çözümü değildir. Bunun yerine bütün jeodezikler için doğru olan ilişkiler (Raychaudhuri denklemleri gibi) ve maddenin doğası (genelde enerji koşulları kalıbında kullanılır) hakkında özel olmayan varsayımlar genel sonuçları türetmek için kullanılır.
Ufuklar
Temel metin: Ufuk (genel görelilik ve kara delik mekaniği

Evrensel geometriyi kullanarak bazı uzay zamanlar ufuklar olarak adlandırılan ve bir bölgeyi uzay zamanın geri kalanından ayıran, sınırları dâhil etmek için gösterilebilir. En iyi bilinen örnekleri kara deliklerdir: eğer kütle uzayın yeterince yoğun bir bölgesinde sıkıştırılırsa(ilgili ölçek uzunluğu Schwarzchild yarıçapı, halka hipotezi olarak tanımlı) içeriden dışarıya ışık çıkamaz. Bir ışık titreşimini hiçbir cisim geçemediği için içteki bütün madde de hapsolmuştur. Dışarıdan içeriye geçiş hala mümkündür. (bu da kara deliğin ufku yani sınırının fiziksel bir engel olmadığını gösterir)
Kara deliklerin eski çalışmaları Einstein’in denklemlerinin açık çözümlerine (özellikle statik bir kara deliği tanımlamak için kullanılan küresel olarak simetrik Schwarzschild çözümü ve dönen statik bir kara deliği tanımlamak ve dönen bir kara deliğin dışındaki bir bölge gibi ilginç özellikleri tanıştıran) simetrik eksenli yapılı Kerr çözümüne güvenildi. Evrensel geometriyi kullanarak sonraki çalışmalar kara deliklerin daha genel özelliklerini gösterdi. Bunlar, enerji, çizgisel moment, açısal moment, belir bir zamandaki yerİ ve elektrik yükünü belirten on bir parametre ile karakterize edilen daha basit cisimlerdir. Bu kara delik eşsizliği teoremi ile belirtilir. (‘’ kara delikler life sahip değildir, bu da insanların saçından bir farkının olmadığını işaret eder)Bir kara delik oluşturmak için çöken kütleçekimsel bir cismin karışıklığına bakmazsak cisim daha basit olur.
Daha önemli bir biçimde termodinamik yasasına benzeyen kara delik mekaniği olarak bilinen yasaların genel bir topluluğu vardır. Mesela kara delik mekaniğinin ikinci yasası (genel bir kara deliğin olay ufkusunun alanı zamanla hiç azalmayacaktır) termodinamik sistemin entropisine benzerdir. Bu, Penrose metodu kullanılarak dönen bir kara delikten klasik araçlar ile çıkartılabilen enerjiyi kısıtlar. Kara delik mekaniğinin aslında termodinamik yasasının bir altkümesi olması güçlü bir kanıttır. Bu da kara delik mekaniğinin orijinal yasalarının değişimine neden olur. Mesela kara delik mekaniğinin ikinci yasası termodinamiğin ikinci yasasının bir kısmı olduğu için özellikle entropi artarsa kara deliğin alanının azalması mümkündür. Sıfır sıcaklığa sahip olmayan termodinamik cisimlerde olduğu gibi kara delikler termal radyasyon salabilirler. Kısmen klasik hesaplamalar onların aslında Planck’in yasasında sıcaklık rolü oynayan yeryüzü kütleçekimi ile yapabildiğini gösterir. Bu radyasyon Hawking radyasyonu olarak bilinir.
Ufukların diğer türleri de vardır. Genişleyen bir evrende bir gözlemci, geçmişin bazı bölgelerinin (parçacık ufku) gözlemlenemeyeceğini ve geleceğin bazı bölgelerinin etkilenmeyeceğini (olay ufku) bulabilir. Minkowski uzayında bile ivmelenen gözlemci tarafından belirtildiğinde, Unruh radyasyonu olarak bilinen kısmen klasik bir radyasyon ile ilişkili ufuklar olacaktır.
Tuhaflıklar
Genel göreliliğin diğer genel bir özelliği tuhaflık olarak bilinen uzay zaman sınırlarının görünümüdür. Uzay zaman ışıksı ve zamansı jeodezikleri- serbest düşüşte ışık ve parçacıkların yol alabileceği bütün yollar- takip ederek araştırılabilir. Fakat bazı Einstein’in denklemlerinin sonuçları eksik kenarlara(ışığın ve düşen parçacıkların yolunun beklenmedik bir sona vardığı ve geometrinin tam tamamlanmamış olduğu bölge) sahiptir. Daha ilginç durumlarda bunlar, sonsuza kadar giden Ricci sabiti gibi uzay zamanın eğikliğini karakterize eden geometrik niceliklerin olduğu eğiklik tuhaflıklarıdır. Hayat çizgisinin bittiği gelecek tuhaflıkları ile uzay zamanın iyi bilinen örnekleri Schwarzchild çözümü(statik ölümsüz bir kara delik içindeki bir tuhaflığı tanımlayan) ya da ölümsüz ve dönen bir kara delik içindeki halka şeklindeki tuhaflıklara sahip Kerr çözümüdür. Evreni tanımlayan Friedmann-Lemaitre-Robertson-Walker çözümleri ve diğer uzay zamanlar Büyük Patlama isimli hayat çizgisinin başladığı eski tuhaflıklara sahiptir ve bazıları da Büyük Çöküş gibi tuhaflıklara sahiptir. Bu örneklerin fazlaca simetrik olduğu farz edersek (bu yüzlen kolaylaşır) tuhaflıklarının oluşumunun idealleşmenin bir yapaylığı olması caziptir. Evrensel geometrinin metotlarını kullanarak kanıtlanan ünlü tuhaflık teoremleri bunun dışında gerçekçi madde özelliklerine sahip bir maddenin çöküşü, mutlak bir evrede ve genişleyen evrenin geniş bir sınıfının başlangıcında gerçekleştikten sonra, tuhaflıkların genel göreliliğin kapsamlı bir geleceğini söyler. Fakat teoremler, biraz tuhaflıkların özellikleri hakkında ve daha çok kapsamlı yapıların varlıklarını karakterize etmeye adanmış geçerli araştırmalar(hipotezi kurulan BKL varsayım isimli örneği) hakkındadır. kozmik sansür hipotezi, bütün gelecek tuhaflıkları (harika bir simetrisi olmayan gerçek özellikli madde) güvenlice ufkunun arkasında saklanır ve bu yüzden bütün uzak gözlemcilere görünmezdir. Henüz düzgün bir kanıt olmamasına rağmen numarasal benzetmeler geçerliliğine destekleyici kanıtlar sunar.
Evrim denklemleri
Temel metin: İlk değeri formülleştirme (genel görelilik
Einstein’in denklemlerinin her bir çözümü bir evrenin bütün tarihini kuşatır. (şeylerin nasıl olduğunun sadece anlık bir fotoğrafı değildir; fakat bütün, mümkün ve madde dolu uzay zamandır) Her yerdeki geometrinin ve maddenin durumunu tarif eder. Genel eşdeğişkenlik nedeni ile Einstein’in teorisi kendince metrik tensörünün zaman evrimini saptaması için yeterli değildir. Koordinat koşulu ile birleştirilebilir. (diğer alan teorilerindeki kapsam sabitlemeye benzer) kısmi türevlenebilir denklemler olarak Einstein’in denklemlerini anlamak için onları evrenin evrimini tanımlayan bir yolda formülleştirmek yararlı olacaktır. Bu, uzay zamanın üç uzay boyutları ve bir zaman boyutuna bölündüğü “3+1” ile adlandırılan formüller ile yapılır. En bilinen örneği ADM biçimciliğidir. Bu bozulmalar, genel göreliliğin uzay zaman evrim denklemleri, ilk koşullar belirtildikten sonra iyi huyludur, her zaman vardır ve eşsizce tanımlıdır. Einstein’in alan denklemlerinin böyle formülleştirmeleri numarasal göreliliğin temelidir.
Evrensel ve hemen hemen yerel nitelikler
Evrim denklemlerinin görüşü derinden genel göreli fiziğin diğer yönü ile bağlanmıştır. Einstein’in teorisinde bir sistemin toplam kütlesi ya da enerjisi gibi görünüşte basit görünen genel bir tanım bulmak mümkün değildir. Temel nedeni, herhangi bir fiziksel alan gibi kütleçekimsel alan belli bir enerji ile verilmesidir; fakat o enerjiyi yerelleştirmenin imkânsız olduğunu temel olarak kanıtlar.
Yine de, kuramsal bir sonsuz uzak gözlemci ya da uygun simetrileri Komar kütlesi kullanarak bir sistemin toplam kütlesini tanımlamanın olasılıkları vardır. Eğer kütleçekimsel dalgalar ile enerjiyi sonsuza taşıyarak sistemin toplam kütlesinden dışarı çıkartırsak sonuç önemsiz sonsuzluktaki Bondi kütlesidir. Klasik fizikse olduğu gibi kütlelerin pozitif olduğu gösterilebilir. Evrensel tutarlı tanımlar momentum ve açısal momentum için vardır. Ayrıca o sistemi içeren uzayın sonlu bir bölgesinde tanımlanan nitelikleri kullanarak formülleştirilen izole edilmiş bir kütle gibi, hemen hemen yerel nitelikleri tanımlamak için birçok çaba vardır. Çember tahmininin daha hassas bir formülleştirmesi gibi izole edilmiş sistemler hakkındaki genel açıklamalar için, amaç yararlı bir nitelik elde etmektir.
Mevcut durum
Genel görelilik, şimdiye kadar pek çok kesin gözlemsel ve deneysel testten geçmiş, son derece başarılı bir kütleçekim ve kozmoloji modeli olarak ortaya çıkmıştır. Bununla birlikte, teorinin eksik olduğu yönünde kuvvetli göstergeler vardır.[14] Kuantum kütleçekimi sorunu ve uzay-zaman tekilliklerinin gerçek olup olmadığı hâlâ belirsizliğini korumaktadır.[15] Karanlık enerji ve karanlık madde için kanıt olarak alınan gözlemsel veriler, yeni fizik teorilerine ihtiyaç duyulduğuna işaret ediyor olabilir.[16]
Bu haliyle bile genel görelilik, daha fazla keşif için zengin olanaklar sunmaktadır. Genel göreliliğin matematiksel alanına yoğunlaşan bilim insanları, tekilliklerin doğasını ve Einstein denklemlerinin temel özelliklerini anlamaya çalışırken[17] göreliliğin sayısal alanına odaklananlar giderek daha güçlü bilgisayar simülasyonları (birleşen kara deliklerin modellenmesi gibi) yürütmektedir.[18] Şubat 2016’da, yerçekimsel dalgaların 14 Eylül 2015’te Gelişmiş LIGO ekibi tarafından doğrudan tespit edildiği açıklandı.[19][20] Ortaya konulmasından bir asır sonra bile, günümüzde genel görelilik hâlâ oldukça aktif bir araştırma alanıdır.[21]
- 1919 – Uluslararası Çalışma Örgütü (ILO) kuruldu.
- 1919 – Singapur, Büyük Britanya ve İrlanda Birleşik Krallığı’ndan bağımsızlığını ilân etti.
- 1919 – 15. Kolordu Komutanlığına atanan Kâzım Karabekir Paşa, Mustafa Kemal Paşa’yı Şişli’deki evinde ziyaret etti.
- 1920 – Damat Ferid, Kuvâ-yi Milliye aleyhinde bildiri yayınladı.
- 1920 – Meclis-i Mebûsan kapatıldı.
- 1930 – Sultanahmet’te büyük kadın mitingi yapıldı. Türk Kadınlar Birliği’nin düzenlediği mitingde, “kadınlara seçme ve seçilme hakkı tanınması” kutlandı.
- 1939 – İngiltere’den alınacak 58 lokomotifin teslimine ilişkin sözleşme imzalandı.
- 1957 – Halk gazetesi sahibi Ratip Tahir Burak, bir karikatürü nedeniyle tutuklandı.
- 1963 – Türkiye Zirai Donatım Kurumu (TZDK) Adapazarı Traktör Fabrikası kuruldu.
- 1965 – ABD’nin orta-batı eyaletlerinde çıkan kasırgalarda 256 kişi öldü.
- 1967 – “Kadınlar I-ıh Derse” adlı oyun İstanbul’da yasaklandı. Başrol oyuncusu Lale Oraloğlu açlık grevine başladı.
- 1970 – Apollo 13 uzaya fırlatıldı.
- 1972 – Kasım 1967’den sonra Amerikan B-52’ler, Vietnam’ı ilk kez yeniden bombalamaya başladılar.
- 1975 – Türk-Irak petrol boru hattının Irak ayağının yapımına başlandı.
- 1975 – Bursa’da Uludağ, Elazığ’da Fırat, Samsun’da Ondokuz Mayıs ve Konya’da Selçuk Üniversitelerinin kurulmasına ilişkin kanun yürürlüğe girdi.
- 1980 – Yazar Ümit Kaftancıoğlu İstanbul’da öldürüldü. Kaftancıoğlu, İstanbul Radyosu Eğitim-Kültür Yayınları’nda programcıydı. Romanlarında, Doğu Anadolu Bölgesi’ni anlatan yazar, insanın insanla ve doğayla mücadelesine önem verdi. Alevilikteki dedelik kurumunu sorguladığı “Hakullah” röportajıyla Milliyet – Karacan Armağanı’nı kazandı.
- 1983 – Zonguldak Kozlu Kömür Üretim bölgesinin İhsaniye ocağında onarım çalışmaları sırasındaki patlamada, biri mühendis 10 madenci öldü, dokuz kişi de yaralandı.
- 1991 – Terörle Mücadele Yasası kabul edildi.
- 1995 – Güneydoğu Anadolu Projesi (GAP) kapsamında Harran Ovası’na ilk su verildi.
- 1997 – Atatürk Uluslararası Barış Ödülü’nün, Bosna’da görev yapan Türk Barış Gücü’ne verilmesi kararlaştırıldı.
- 2001 – Güney Afrika’da bir maçta taraftarlar arasında çıkan arbedede 43 kişi öldü, 100 kişi yaralandı.
- 2001 – Avustralya ve Amerikan Samoası arasında oynanan maçı, Avustralya 31-0 kazandı.
- 2002 – Tunus’ta bir Sinagog bombalandı; 21 kişi öldü.
- 2006 – İran Devlet Başkanı Mahmut Ahmedinejad, uranyum zenginleştirdiklerini açıkladı.
- 2006 – İtalya’da 43 yıldır kayıp olan ünlü mafya babası Bernardo Provenzano, Corleone köyünde bir koruma ile sebze çorbası içerken yakalandı.
- 2009 – Dev-Genç Birliği kuruldu.
- 2010 – YGS Yükseköğretime Geçiş Sınavı’nın ilki yapıldı.
 Osmanlı Gazetesi Medya İmparatorluğu
Osmanlı Gazetesi Medya İmparatorluğu






















































