
31 Martta ölenler
Ölümler
- 1340 – I. İvan, Moskova Büyük Prensi (d. 1288)
| I. İvan | |
|---|---|
 |
|
| Moskova Büyük Prensi | |
| Hüküm süresi | 21 Kasım 1325 – 31 Mart 1340 veya 1341 |
| Önce gelen | III. Yuri |
| Sonra gelen | Semyon |
| Doğum | 1288 Moskova |
| Ölüm | 31 Mart 1340 veya 1341 (51–53 yaşında) Moskova |
| Defin | Başmelek Katedrali |
| Eş(ler)i | 1.Elena Aleksandra 2.Ulyana |
| Çocuk(lar)ı | Semyon, II. İvan |
| Hanedan | Rurik Hanedanı |
| Babası | Daniil |
| Annesi | Maria |
I. Ivan Daniiloviç Kalita (Rusça: Ива́н I Даниилович Калита; 1288 – 31 Mart 1340 veya 1341) 1325 ile 1340 veya 1341 yılları arasında hüküm sürmüş Moskova Büyük Prensi. Abisi, III. Yuri’nin ölümünden sonra İvan, Moskova Prensliği tahtına çıktı. Ivan, Altın Orda Han’ının onayı ile elde edilebilecek Vladimir Büyük Dükü unvanını alma mücadelesine katıldı. Rakipleri Mikhail, Korkunç Gözlü Dmitry ve Aleksandr Mihayloviç’di. Hepsi Altın Orda’da öldürüldü. 1328’de I. İvan, Özbek Han’ın tüm Rusya topraklarından vergi toplama hakkı ile Vladimir’in Büyük Dükü olma onayını aldı. 31 Mart 1340 veya 1341’de öldüğü sanılıyor.
Hayatı
Ağabeyi Yuri’nin ölümünden sonra İvan’a Moskova Prensliği miras kaldı. İvan, Altın Orda’dan bir hanın onayıyla elde edilebilen Vladimir Büyük Dükü unvanını almak için mücadeleye katıldı. Bu mücadelede Moskova prensinin ana rakipleri Tver prensleriydi – Mikhail, Korkunç Gözlü Dmitry ve Aleksandr Mihayloviç’di. Hepsi Altın Orda’da öldürüldü. 1328 yılında Ivan, tüm Rus topraklarından vergi toplama hakkına sahip Vladimir Büyük Dükü olmak için Özbek Han’ın onayını aldı.[3]
İmparatorluk Rus tarihçisi Vasily Klyuchevsky’ye göre, Moskova’nın Ivan yönetimindeki yükselişi üç faktör tarafından belirlendi. Bunlardan ilki, Moskova Prensliği’nin diğer Rus prensliklerinin ortasında yer almasıydı; böylece Doğu’dan ve Batı’dan gelebilecek her türlü istiladan korunuyordu. Komşuları Ryazan Prensliği ve Tver Prensliği’ne kıyasla Moskova daha az tahribata uğramıştır. Moskova bölgesinin göreceli güvenliği, Moskova’nın yükselişinin ikinci faktörü olan sürekli baskınlardan bıkan ve diğer Rus bölgelerinden aktif olarak Moskova’ya taşınan çalışan ve vergi ödeyen insanların akınına neden oldu. Üçüncü faktör ise Novgorod’dan Volga nehrine uzanan bir ticaret yoluydu.
Baumer’e göre, Özbek Han eski böl ve yönet politikasını terk edip yeni büyük prensi tüm Rus şehirlerinden haraç ve vergilerin toplanıp aktarılmasından sorumlu tutarak kader belirleyici bir karar aldı. İvan bu vergileri zamanında teslim ederek ayrıcalıklı konumunu daha da güçlendirdi. Bu şekilde Moskova’nın bölgesel bir büyük güç olarak geleceğinin temellerini attı.
İvan, Moğolların akınları sırasında ele geçirdikleri Rusları satın alarak insanları prensliğine yerleştirme politikasını bilinçli bir şekilde sürdürdü. Topraklarındaki tüm hırsızları ortadan kaldırmayı başardı ve böylece seyahat eden tüccarların güvenliğini sağladı. Moskova Prensliği’ne Moğol akınlarının olmamasıyla birlikte iç barış ve düzen, Rus kroniklerinde “büyük barış, sessizlik ve Rus topraklarının rahatlaması” olarak bahsedilmiştir.Ivan, Moskova’yı çok zenginleştirdi (bu nedenle Kalita veya Para Çantası lakabını kazanmıştır). Bu zenginliği komşu Rus prensliklerine borç vermek için kullandı.Böylelikle bu şehirler giderek daha da borç batağına düştüler ve bu durum sonunda İvan’ın haleflerinin bu şehirleri ilhak etmesine olanak sağladı. Moskova çevresindeki toprakları satın aldı ve çoğu zaman fakir sahipleri topraklarını kendi istekleriyle sattılar. Bazıları İvan adına topraklarında hüküm sürme hakkını devam ettirdi. Öyle ya da böyle bir dizi şehir ve köy Moskova Prensliği’ne katıldı – 1323’te Ugliç, 1328-1338’de Belozersk Prensliği ve 1340’ta Galiç Prensliği.
Ancak Ivan’ın en büyük başarısı, Saray’daki Han’ı kendi oğlu Semyon’u Vladimir Grandükü olarak yerine geçmesi konusunda ikna etmesiydi ve o andan itibaren bu pozisyon neredeyse her zaman Moskova’nın yönetici hanedanına ait oldu.
1335’te (Moskova-Litvanya Savaşları’nın bir parçası olarak) Torjok kasabasına yapılan bir Litvanya baskınının ardından İvan, Osechki ve Ryasna kasabalarını yakarak misilleme yaptı.
İvan 31 Mart 1340 veya 1341’de Moskova’da öldü. 1 Nisan’da Başmelek Katedrali’ne gömüldü.
Ailesi
Ivan iki kez evlenmiştir. İlk eşinin adı Elena’ydı ve kökeni hakkında tam olarak hiçbir şey bilinmemektedir.
• Semyon Ivanovich (7 Kasım 1316 – 27 Nisan 1353), geleceğin Moskova Grandükü.
• Daniel Ivanovich (11 Aralık 1319/20-1328);
• Fefinia Ivanovna (genç yaşta öldü);
• Maria Ivanovna (2 Haziran 1365’te öldü), 1328’de Rostov Prensi Konstantin ile evlendi;
• İvan İvanoviç (30 Mart 1326 – 13 Kasım 1359), geleceğin Moskova Grandükü;
• Andrei Ivanovich (4 Ağustos 1327 – 6 Haziran 1353), Novgorod Prensi;
• Evdokia Ivanovna (1314 – 1342), Yaroslavl Prensi Vasili Mikhailovich ile evliydi.
• Feodosia Ivanovna (1389’da öldü), Belozersky Prensi Fyodor Romanovich ile evlendi.
Prenses Elena 1 Mart 1331’de öldü. Bir yıl sonra İvan tekrar evlendi, ancak ikinci eşinin sadece adı bilinmektedir: Ulyana.
- 1461 – Metropolit Jonah, 1448’den 1461’e Kiev ve Tüm Rusya Metropoliti idi (d. 1390)
| Metropolit Jonah | |
|---|---|
| Moskova metropoliti | |
 |
|
| Kilise | Doğu Ortodoks Kilisesi |
| Makam | Moskova |
| Görevlendiriliş | 1448 |
| Dönem bitişi | 1461 |
| Önce gelen | Kievli İsidoros |
| Sonra gelen | Theodosius |
| Doğum | 1390s |
| Ölüm | 31 March 1461 Moskova, Moskova Knezliği |

Metropolit Jonah (d. 1390’lar, Odnoushevo kilise bahçesi – şimdi Kostroma bölgesinin Soligalichsky bölgesi – ; ö. 31 Mart 1461, Moskova, Moskova Knezliği) 1448’den 1461’e Kiev ve Tüm Rusya Metropoliti idi. 1547’de Makarievsky Katedralinin kararıyla aziz ilan edilen Jonah Birleşik Rus Kilisesi’ne ve Kiev ve Tüm Rusya Metropolitliği’nin başkanlık eden son metropolittir.

Biyografi

1390’larda Kazan topraklarının sınırına yakın, Vyatka Nehri’nde Soligalich’e 6 verst uzaklıkta olan Galiç şehrinin Odnoushevo köyünde, Theodore Odnoush adında hizmetçi ve dindar bir babadan doğdu. 12 yaşındayken Galiç yakınlarındaki Müjde Manastırı’nda manastır oldu. Birkaç yıl sonra, Simonov Manastırı’na’ (Moskova) taşındı. 1431’den sonra Ryazan ve Murom Piskoposu oldu.

Metropolit Photius’un 1431’de ölümü üzerine, fiilen Rus Kilisesi’ne başkanlık etti: 1432’de “Rusya’nın En Kutsal Metropoliti” olarak adlandırıldı. Bununla birlikte, Büyük Dük’ün tahtı için verilen iç mücadele, azizin Konstantinopolis’e, kutsanma için Patrik II. Yusuf’a gitmesine izin vermedi. Bu arada, 1433 sonbaharında, Litvanya prensi Švitrigaila, Smolensk Piskoposu Gerasim’i Metropolitan olarak kutsanması için İstanbul’a gönderdi. Gerasim, Konstantinopolis’te Tüm Rusya Metropoliti rütbesine yükseltildi; ancak 1435’te Prens Švitrigaila tarafından ihanetten şüphelenilerek idam edildi. Metropolit Gerasim’in ölümünden sonra Piskopos Jonah Konstantinopolis’e gitti; ancak 1437’de İmparatorluğun başkentine vardığında, 1436’da Patrik Yusuf’un İsidoros’u Rus metropolitliğine atadığını öğrendi.
15 Aralık 1448’de Moskova’daki Rus Piskoposlar Konseyi’nde Kiev ve Tüm Rusya Metropoliti seçildi. Adaylığı Konstantinopolis’deki Patrik’in kararıyla uyumsuzdu; bununla birlikte, İstanbul’da post factum bir kutsama alacağı varsayılmıştır. Ancak Piskopos Jonah, kutsama için Konstantinopolis’e gitmeyi başaramadı. Bu Floransa Konsili’ni reddeden Rus Ortodoks Kilisesi’nin İstanbul Rum Ortodoks Patrikhanesi’nden otosefalisinin başlangıcı olarak kabul edilir.
1458’de Moskova, Litvanyalı diplomat Ivashents tarafından getirilen Metropolit İsidoros’un öğrencisi olan Bulgar Metropolit Gregorios’un metropolitliğini reddetti.
1459’da, Moskova prensinin rızasıyla Rus Piskoposlar Konseyi’nin metropolit seçimi için yeni bir prosedür belirlenmesi de otosefaliyi derinleştirdi.
Jonah kalıcı olarak Moskova’da yaşadı ve Moskova’da bir katedrale sahip olan, ancak Kiev Metropoliti unvanını taşıyan son aziz oldu.
Metropolit Jonah, Büyük Dük II. Vasili üzerinde büyük bir etkiye sahipti, dağınık Rus beyliklerini birleştirmek için faaliyetlerine aktif olarak katıldı.
Metropolit Jonah’ın altında, 1431’de başlayan Chudov Manastırı’nın yeniden inşası sırasında kalıntıları bulunan ve yerel olarak saygı duyulan Metropolit Alexy ve Radonezh Sergius, Rus Kilisesi’nin azizleri olarak ciddiyetle kanonlaştırıldı.
31 Mart 1461’de öldü.
Saygı
27 Mayıs 1472’de, Cüppelerin Göğe Kabulü Kilisesi’nin yeniden inşası sırasında, kalıntıları bulundu; Pachomius onun için bir kilise ayini yazdı. 1547’de Metropolit Macarius yönetiminde, daha da yüceltildi.
1596’da Patrik Job, 5 Ekim’de diğer Moskova’daki Uyu Hali (İngilizce:Dormition) Katedrali’nde Aziz Jonah’ın kutlamasını başlattı.
- 1547 – I. François, 1515 ile 1547 yılları arasında hüküm süren Fransa Kralı (d. 1494)
| I. François | |
|---|---|
 |
|
| Fransa kralı | |
| Hüküm süresi | 1 Ocak 1515 – 31 Mart 1547 |
| Taç giymesi | 25 Ocak 1515, Reims |
| Önce gelen | XII. Louis |
| Sonra gelen | II. Henri |
| Doğum | 12 Eylül 1494 Cognac, Charente, Fransa |
| Ölüm | 31 Mart 1547 (52 yaşında) Château de Rambouillet |
| Defin | Saint-Denis Bazilikası, Fransa |
| Eş(ler)i | Claude de France (e.1514-öldü 1524) Habsburglu Eleanor(e.1530) |
| Çocuk(lar)ı | Bretonlu III. François II. Henri Madeleine, İskoçya Kraliçesi Charles, Orléans Dükü Margaret, Savoy Düşesi |
| Hanedan | Valois Hanedanı |
| Babası | Charles d’Orléans, Angoulême Kontu |
| Annesi | Louise de Savoie |
| İmza |  |
I. François (okunuşu: [fʁɑ̃.swa], Fransızca: François Ier) (d. 12 Eylül 1494, Cognac – ö. 31 Mart 1547, Château de Rambouillet), 1515 ile 1547 yılları arasında hüküm süren Fransa Kralı. Valois Hanedanının Angoulême kolundan gelen beş hükümdardan ilkidir.
I. François sanat ve edebiyat alanlarındaki gelişmeleri teşvik ederek Fransa’da rönesans ve hümanizmin yayılmasında yardımcı oldu. Saray için yapılan mimari eserleri yetenekli İtalyan sanatçılara teslim etti. Yaptırdığı krallık sarayları ve konakları, burjuva konaklarına örnek olmuştur. Edebiyata da önem veren I. François, hümanist yazarların eserlerinin çevrilmesine ve yayılmasına katkıda bulundu. Clément Marot gibi yazarları koruması altına aldı. I. François sosyal bilimler üzerine araştırma yapan ilk Fransız üniversitelerinden biri olan Collège de France’ın kurucusudur.
I. François Batı Avrupa’da İngiltere ve Kutsal Roma Cermen İmparatorluğu ile rekabete girmişti. Bu ülkelere karşı Osmanlı İmparatoru Kanuni Sultan Süleyman ile ittifak yaptı.
Yaşamı
Gençliği ve Tahta Çıkışı
Angoulême kontu Charles d’Orléans ile Louise de Savoie’nın oğluydu. Babasının kuzeni XII. Louis’nin 1498’de tahta çıkması üzerine tahtın varisleri arasına girdi ve Valois dükü oldu. François’ya güvenmeyen XII. Louis, onu devlet işlerine karıştırmadı ve henüz 18 yaşındayken saldırı altındaki sınır bölgelerine gönderdi. Ölümünden kısa süre önce de François’yı 15 yaşındaki kızı Claude ile evlendirdi (1514). 1524’te dul kalan François, 1530’da V. Karl’ın kızkardeşi Habsburglu Eleanor ile evlendi. François, XII. Louis’nin ölümünden sonra, 1 Ocak 1515’te Fransa kralı oldu.
Hükümdarlığı

Devlet yönetimindeki deneyimsizliğini işlek ve keskin zekası, inanılmaz belleği ve öğrenme tutkusuyla kapattı. Ama dost canlısı olması, herkese güvenmesi ve düşüncelerini gizlemeyi becerememesi yüzünden iyi bir siyaset adamı olamadı.
İç Politika
François, XII. Louis ve oğlu II. Henri ile birlikte modern Fransız devletinin kurucularından sayılır; Fransa tarihinin dönüm noktalarından birine, XVI. yy.’ın ilk yarısına kişisel damgasını vurdu. Krallık dönemi bir bolluk ve büyüme evresi oldu. Bu zenginlik dönemini değerlendiren François, vergi sistemini geliştirerek, siyasal gücünü artırdı. XVI. yy.’ın başında oluşan merkantalist düşüncelerin etkisinde kalarak XI. Louis gibi o da, sanayi ve ticarete el attı. Yeni dökümhaneler ve demir atölyeleri kurdurarak topçu birliklerinin giderek artan isteklerini karşıladı. Saint-Étienne’de bir silah yapımevi kurdurdu, aynı dönemde egemen sınıfların lüks tüketim gereksinimlerini karşılayan bir dizi ipek ve cam imalathanesi kuruldu. Paris ve Lyon matbaa işçilerinin grevi (1539-1541) Kral’a işçi ayaklanmalarını bastırmak için önlemler alma fırsatı verdi. Villers-Cotterêts Fermanıyla (1539), işçilerin lonca ve birliklerde örgütlenmeleri yasaklandı. Bu önlemler efendilerin tüccar burjuvazisinin çıkarlarına uygun düşmekteydi.
François, bu refah döneminden yararlanarak, modern bir devletin merkezi yapısını oluşturma yönünde önemli adımlar attı. Var olan kurumların yapısını değiştirerek ve bir dizi reformla monarşinin otoritesini güçlendirdi, merkezci bir yönetim oluşturmak için gerekli önlemleri aldı. Tahtta kaldığı sürece États généraux’yu hiç toplamayan François, Parlamentonun siyasi gücünü de 24 Temmuz 1527 fermanıyla ortadan kaldırdı. Bourbon connétable’inin ihanetine onun fief’ini Fransa topraklarına katarak karşılık verdi (1531), Bretonya’yı kesin olarak krallığa bağladı (1532).
François yaz kış Fransa’yı at sırtında dolaşarak, yaşamlarında hiç kral görmemiş olan halkının karşısına çıktı. Yolculukları sırasında cezaevlerini boşalttı, yargı gücünün soylularca kötüye kullanılmasını önlemeye çalıştı, cömert ihsanlarda bulundu. Yargı sistemini de ıslah ederek valilik ve derebeylik mahkemelerinin yetkilerini artırdı (1536 Crémieu Fermanı), ağır ceza hukukunu kurallara bağladı, kilise mahkemelerinin yetkilerini kısıtladı, tüm yargı hükümlerinin ve noter belgelerinin Fransızca yazılmasını zorunlu kıldı, papazlara vaftiz ve cenazeler için kayıt tutma zorunluluğunu getirdi. Devlet hazinesi yerini tutan Tasarruf Sandığı’nı kurdu (1523), ancak askeri giderler ve debdebeli bir saray yaşamının masrafları karşısında başka kaynaklara başvurmak zorunda kaldı.
Din Politikaları
Ülkeyi öbür Avrupa ülkelerinin hükümdarlarınınkinden çok daha güçlü bir otoriteyle yönetmeye başladı. Bologna Antlaşması (1516) ile Kilise’ye boyun eğdirdi, rahip, piskopos ve başpiskopos atama yetkisini aldı; soyluları sarayda denetimi altında tutarak onları iktidarının bir parçası durumuna getirdi, taşra beyliklerini de sıkı denetim altında tuttu.
Fransa’da din mücadeleleri baş gösterince, hoşgörülü dünya görüşünü sürdüren François, ülkede artan bağnazlığı yatıştırmaya çalıştı. Bakanlarının katı Katolik olmaları ve dinsel alanda kişisel seçimini kullanarak, Reform hareketine karşı çıktıysa da kız kardeşi Marguerite d’Angoulême’in etkisi ve Hristiyanlığın insancıl öğretisine olan inancıyla krallığın tüm bölgelerine ve toplumun tüm katmanlarına yayılmış olan Reform yanlılarına hoşgörü gösterdi.
Ancak dinsel inancın krallığın en önemli birleştirici öğesi olduğunu ve Reform hareketinin bölücü yanlarının ağır bastığını düşünerek sonunda sert bir baskı politikası uygulamaya başladı. Cumhuriyet yanlısı olarak görülen Reformcular çok geçmeden kazığa bağlanıp yakılmaya başladı. François, Valdocu Protestan tarikatın ortadan kaldırılmasını beş yıl geciktirdiyse de yok etme emrini ölüm döşeğinde, okumadan imzaladı.
Edebiyat’ın Hamisi

I. François sanat ve edebiyat alanlarında da kişisel etkisini göstererek Fransa’da Rönesans ve hümanizmin yayılmasına yardımcı oldu. Krallık debdebesi onun döneminde çok arttı, çeşitli saraylar ve konaklar yaptırıldı. Saray için yaptırılan veya onarılan tüm yapıları İtalyan sanatçılara teslim etti, krallık yapıları soyluların ve burjuvaların konaklarına örnek oldu. “Edebiyat’ın Hamisi” (Le protecteur des Lettres) olarak anılan François, hümanistlerin çevrilmesi ve yayımlanmasını (Guillaume Budé) destekledi ve geleceğin Collège de France’ını kurdu (1530).
Dış Politika

I. François’nın krallığının önemli bir bölümü dış politikayla geçti. Bu politikanın başlıca amacı; XII. Louis’in 1513’te kaybettiği Milano bölgesini yeniden ele geçirmekti. XII. Louis, Milano Dükalığı’nı geri almak üzere hazırlanmış bir ordu bırakmıştı. Büyükbabasının annesi Valentina Visconti’den kalan ve durmaksızın el değiştiren bu mirası yeniden ele geçirme isteği François’yı sardı. Çevresindeki genç soyluların da yüreklendirdiği François, komşularıyla barışı güvence altına aldıktan sonra İtalya üzerine yürüdü. Kanlı Marignano Çarpışması’nda (1515) süvarilerinin başına geçerek Dük Massimilano Sforza ve müttefiki Papa X. Leo’nun kiraladığı ve yenilmezliğiyle ün salmış paralı İsviçre askerlerini bozguna uğrattı. Papa, François’yı Bologna’da göz kamaştırıcı bir biçimde ağırlayarak değerli armağanlar verdi. Varılan anlaşma uyarınca Papa Fransız Kilisesi’nin beneficium’larını (geliri belirli bir kilise kademesine ayrılmış toprak mülkü) yeniden elde ederken, piskoposların atanması krala kalıyordu. Böylece François, fazlasıyla mülk edinerek bağımsızlaşmış din adamları üzerindeki otoritesini güçlendirmeyi başarmış oluyordu.
Sarayını başyapıtlarıyla donatan, Leonardo da Vinci ve Sforza gibi sanatçılara cömertçe mülkler bağışlayan François, İsviçrelilerle bir sürekli barış anlaşması imzaladıktan sonra İsviçreliler paralı asker olarak kralın ordusuna katılmaya başladı. Bu antlaşmalar ilk İtalya Savaşlarına son verdi. İngiltere kralı VIII. Henry’den Tournai’yi geri aldı. 1516 yılında, 16 yaşındayken İspanya kralı olan, Felemenk topraklarının varisi Habsburglu Carlos’la (sonradan Kutsal Roma-Germen imparatoru ve François’nın baş düşmanı olan V. Karl) Noyon Antlaşması’nı imzaladı. Ayrıca tahta çıktıktan sonra doğan ilk kızı Prenses Louise’le nişanladı ve Napoli üzerindeki haklarını vermeyi vadetti.
Halkının artık yakından tanıyıp bağlandığı François, Kutsal Roma-Germen imparatoru Maximillian’ın öldüğü 1519 yılında bütün Hristiyan dünyasının en güçlü hükümdarıydı. Maximilian’ın torunu Karl’ın imparator olması ise François için bir yıkım oldu; Zaten İspanya kralı olan Karl, şimdi elinde bulundurduğu topraklarla bütün Fransa’yı kuşatmış bulunuyordu.
V. Karl’ın (Şarlken) evrensel bir monarşi kurma projesinin karşısındaki en büyük engel ise Fransa kralıydı. Altın Çadırlı Ordugah görüşmelerinde (1520) İngiltere kralı VIII. Henry’nin desteğini sağlamaya çalışan ancak başaramayan I. François savaşı başlatan taraf oldu. V. Karl ile Fransa arasındaki çatışmalar 1521’de kuzeyde ve Pireneler’de başladı. Fransız ordusu, askerlerin ücretleri ödenemediği için dağılmak üzereydi. François danışmanlarına kulak vermiyor, emirlerinin yerine getirilip getirilmediğiyle de ilgilenmiyordu. Yolsuzlukların önüne geçmek için birkaç vekilharcının idam edilmesine karşın hazine durmadan boşalıyordu.
1523’te François, Bourbon 8. dükü III. Charles’ın karısının mirası olarak kabul edilen geniş Bourbon topraklarını dükten geri istedi. Bu isteğe uymadığı için topraklarına el konan Charles, krala ihanet ederek V. Karl’ın hizmetine girdi. Karl’ın imparatorluk ordusunun başına geçen Charles’ın, Provence’ı istila girişimi Marsilya yakınlarında durduruldu ve Charles İtalya’ya doğru geri çekilmek zorunda kaldı. Ama İngilizler ile Almanlar kuzeyde ilerliyordu. Sonunda François 1525’teki Pavia Çarpışması’nda yenilgiye uğrayarak yaralı durumda esir düştü.

Yavuz Sultan Selim’in saltanatı boyunca duraksayan Osmanlı’nın Avrupa’daki genişlemesi Kanuni Sultan Süleyman döneminde yeniden başlamıştı. Osmanlı İmparatorluğu için batıda en ciddi tehlike Kutsal-Roma Cermen (Habsburg) İmparatorluğu’dur. İmparator Şarlken (V. Karl) Macaristan’ı da nüfuzu altına almıştır.
Habsburg Hanedanının rakibi Fransa Kralı I. François’nın 1526’da Pavia’da Kutsal-Roma Cermen İmparatoru Şarlken’e yenilerek esir düşmesi ve Kanuni’nin Şarlken’in gücünü kırmak için François’ya yardım etmesi, gereken fırsatı doğuran etkenlerden biridir. Çünkü I. François’nın esareti, Roma-Germen İmparatorluğu’na Avrupa’da daha çok üstünlük sağlamış, Şarlken’in bu çabalarına Macaristan da destek vermiştir.
Tutsaklığı sırasında annesi, Osmanlı Sultanı Kanuni Sultan Süleyman’a bir elçiyle, kendi ve oğlu adına iki mektup göndererek V. Karl’a karşı savaşta yardım istedi; Macaristan’a sefer yapılmasını önerdi. Kanuni, gönderdiği yanıtta, François’ya, France Vilayeti kralı olarak hitap etti. Kralların yenilip tutsak olabileceklerini, gönlünü hoş tutmasını, düşmanı kovmak ve ülke fethetmek için her zaman hazır olduklarını yazdı. Ardından Mohaç Seferi’ne çıktı (1526).
François’yı serbest bırakmanın bedeli olarak V. Karl, Fransa’nın üçte birinin kendisine verilmesini, bu ülkenin İtalya üzerindeki hak iddiasından vazgeçmesini, Bourbon düküne topraklarının geri verilmesini ve bunlara Provence’nin de eklenmesini istedi. François buna, “krallığıma zarar verecek koşulları kabul etmektense Tanrı’nın layık gördüğü sürece hapiste kalmaya kararlıyım” biçiminde karşılık verdi. Madrid’de bir kuleye hapsedilen kral, ağır yenilgi, ülkesinin içinde bulunduğu tehlikeli durum, tutsaklık, vücudundaki eski yaralar ve yeni tutulduğu frengi yüzünden sağlığını yitirdi. Sonunda iyileşti ama kişiliğinde önemli tutarsızlıklar ortaya çıktı.
V. Karl sınır tanımayan isteklerinde ısrarlıydı. Hapishanede ölmeye kararlı olan François, en büyük oğlu lehine tahtta feragat etti. Bu karar Fransa’da kötü karşılandı. François’nın yurduna dönmesini sağlamak üzere onun adına hareket eden elçiler, Karl ile çok ağır koşullar taşıyan Madrid Antlaşması’nı imzaladılar. Bu antlaşmayla Milano, Napoli, Cenova ve Asti üzerindeki haklarından, Flandre ve Artois üzerindeki hükümranlığından vazgeçiyor, Bourgogne’u V. Karl’a geri veriyordu. François ise Ocak 1526’da antlaşmayı onaylarken, tutsak bir şövalyenin imzasının geçersiz olduğunu ve krallığın parçalamaya kendi gücünün de yetmeyeceğini söyledi. Ama hasta yatağında yatarken, antlaşma hükümleri çerçevesinde iki hükümdarın uzlaşmasının bir göstergesi olarak, Portekiz kralının dul eşi ve Karl’ın kız kardeşi Eleanor’la nişanlandı. Antlaşmanın son koşulu olarak da yedi ve sekiz yaşlarındaki en büyük iki oğlunu rehine olarak bıraktı.
Ancak François serbest kalınca sözünde durmadı. Teslim edilen eyaletler Fransa’dan ayrılmayı reddettiler. Papalık, Venedik, Floransa ve Milano ile Cognac Birliği’ni (1526) kurarak Avrupa’daki güç dengesini düzeltmeye çalıştı; VIII. Henry ile bir “ebedi barış” imzaladı (1527). Yemininden dönen krala öfkelenen V. Karl, çocukları dört yıl hapiste tuttu. Karl’ın ordusu İtalya’yı yağmalayarak Papa VII. Clemens’i tutsak aldı. François, V. Karl’a karşı her yerde patlak veren savaşlara açıkça katılabilecek ve örneğin Osmanlılar gibi gizli müttefiklerine verdiği sözleri yerine getirebilecek durumda değildi. Mohaç Savaşı’ndan sonra Avrupa’da Türkler’e karşı güçlenen tepkiden ve V. Karl’ın kendisini Hristiyan dünyasına karşı Müslüman Türklerle ittifak halinde göstermesinden çekinerek Osmanlılar’la anlaşmasını bir süre gizledi. Onların yolladıkları elçilerden kaçmak için ormanlarda uzun av gezilerine çıkıyor, ülke içindeki yolculukları sırasında yalnızca birkaç gün kalacağı şatolar yaptırıyordu. Collège de France da bu sırada kuruldu. Gönderdiği elçilerle Kanuni’nin Almanya Seferi’ne (1532) çıkmasını engellemeye çalıştı. Kanuni kendisini ve Papa’yı hapseden V. Karl’a karşı savaşmasını engellemeye çalışmasını şaşkınlıkla karşıladığını, üstelik Belgrad’a varmış ordunun geri dönmesine olanak bulunmadığını bildirdi.
Aralarındaki derin nefret, Karl ile François’nın birbirlerini düelloya çağırmalarına bile yol açtı, ama düello önlendi. Kralın sarayın uzağında olduğu bir sırada annesi, Karl’ın halası Margaret ile bu ölümcül mücadeleyi durdurmak üzere bir antlaşmaya vardı. Bunun sonucunda 1529’da imzalanan Cambrai Antlaşması, Madrid Antlaşması’nın koşullarını hafifletiyordu. Çocuklarını geri alması için François’nın müttefiklerinden ayrılması, İtalya’dan vazgeçmesi ve 2 milyon altın kuron ödemesi gerekiyordu. François’nın hesapsız harcamaları yüzünden hazine boşaldığından tazminat bedeli zorla toplanabildi. Ama sonunda küçük prensler, babaları 1530’da Eleanor’la siyaset gereği evlenirken serbest kaldılar.
François, V. Karl’a karşı siyasal girişimlerini sürdürdü. 1532’de Scheyern Antlaşması ile Smalkade Birliği üyesi Alman Protestan prensleriyle ittifak kurdu. 1535’te Fransa ile Osmanlı Devleti arasında ilk ticari ve hukuki ayrıcalık anlaşmaları (kapitülasyonlar) imzalandı. Bu antlaşmalarla Osmanlı ülkesinde ticaret yapacak Fransızlar’a, Fransız bayrağı taşıyan gemilere ayrıcalık tanındı.
Osmanlılarla ilk ticaret antlaşmasının imzalanmasından (1535) sonra durumunu güçlendiren François, V. Karl’a karşı yeniden savaş açtı. Ancak 1536-38 ve 1542-44 yılları arasında yer alan iki yeni savaşta da önemli bir kazanç sağlayamadı. Crépy-en-Laonnois Antlaşması’yla (1544) Flandre ve Artois üzerindeki hükümdarlığından vazgeçtiğini onayladı; ancak Bourgogne’u geri aldı. François’nın son diplomatik başarılarından biri, 1525’ten beri ilişki içinde olduğu Osmanlılarla Karl’a karşı resmen ittifak kurmak oldu. Bu savaş sırasında Kaptan-ı derya Barbaros Hayreddin Paşa komutasında bir donanma, küçük Fransız donanmasıyla birlikte Nice kentini kuşattı ve ele geçirerek Fransa’ya bıraktı (1543).
Bu arada aile içindeki felaketler de birbirini izlemeye başlamıştı. Veliaht 18 yaşında öldü. Kralın en sevdiği üçüncü oğlu da vebadan öldü.
Ölümü
François’nın ölümünden önceki son önemli uygulamaları arasında Le Havre limanını kurmak, Jacques Cartier’yi Kanada’ya göndermek, yargı sistemini gözden geçirmek ve bütün yasal belgelerde Fransızca kullanılması için ferman çıkartmak sayılabilir. François, yaşamının son yıllarında Kutsal Roma Cermen İmparatorluğu’nun gücünü sınırlamış, ancak İtalya ile ilgili planlarını gerçekleştirememişti. Ardlı II. Henri de onun hedeflerini benimsedi ve V. Karl’la savaşı sürdürdü.
- 1621 – III. Felipe, İspanya, Portekiz, (II. Felipe adıyla) Napoli, Sicilya, Sardinya kralı ve Milano dükü (d. 1578)
| III. Felipe | |
|---|---|
 |
|
| İspanya ve Portekiz kralı | |
| Hüküm süresi | 13 Eylül 1598 – 31 Mart 1621 |
| Taç giymesi | 13 Eylül 1598 |
| Önce gelen | II. Felipe |
| Sonra gelen | IV. Felipe |
| Doğum | 14 Nisan 1578 Madrid, İspanya |
| Ölüm | 31 Mart 1621 (42 yaşında) Madrid, İspanya |
| Defin | El Escorial |
| Eş(ler)i | Avusturyalı Margaret |
| Babası | II. Felipe |
| Annesi | Anna (Avusturya) |
| Dini | Roma Katolik Kilisesi |
| İmza | 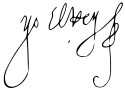 |
III. Felipe (İspanyolca: Felipe III; 14 Nisan 1578, Madrid – 31 Mart 1621, Madrid, İspanya), İspanya, Portekiz, (II. Felipe adıyla) Napoli, Sicilya, Sardinya kralı, Milano dükü, Belçika Hollandası, Comté ve Şarole hükümdarı (1598-1621).
Hayatı


İspanya kralı II. Felipe ile Habsburg Hanedanından Avusturya prensesi Anna’nın oğludur. Dindar, iyiliksever ve kişisel ilişkilerinde son derece dürüst bir kişi olmasına karşın, 13 Eylül 1598 tarihinde tahta geçtikten sonra sorumsuz ve gevşek bir yönetim gösterdi.
Nisan 1599’da Habsburg Hanedanından kuzeni, Avusturya arşidüşesi Margaret ile evlendi, sekiz çocukları oldu.
Devlet işlerini, valido olarak adlandırılan gözdelerinden Lerma Markisi Gómez de Sandoval y Rojas’a bıraktı. Daha sonra Lerma Dükü oldu.
Felipe döneminde Osmanlılara karşı düşmanlık politikasını sürdüren ve İtalya’da Venedik Cumhuriyeti ve Savoie Dükalığı’yla çekişme içine giren İspanya, Avrupa’nın geri kalan ülkeleri ile uzlaşmacı bir politika tercih etti. Fransa ile kurulan iyi ilişkiler, İspanya’ya, İtalya’da (Savoia [1614-1617] ve Venedik’e [1613-1617] karşı savaşlar) ve özellikle Kutsal Roma-Germen İmparatorluğu’nda (1616’da II. Ferdinand’ın, Avusturya’ya ait Alsas topraklarından vazgeçme vaadi) daha etkin bir rol oynama olanağını verdi. 1618’de Otuz Yıl Savaşı’nın patlak vermesiyle batıdaki savaş dönemi sona erdi. Fakat savaş ilerledikçe zaman içinde Felipe, Kutsal Roma-Germen İmparatoru II. Ferdinand ve Katolik Alman prenslerine destek verdi.
Felipe 1618’de Lerma dükünü görevden alıp, Uceda dükü olan oğlunu yerine geçirdi.


Bu barış ortamı yönetime Hristiyanlaşmış Endülüs Müslümanlarının (Moriskolar) üstesinden gelme olanağı verdi. 9 Nisan 1609’da Endülüs Müslümanlarının ülkeden sürülmesi kararı alındı. Bu uygulama İspanya’da iç birliği ve barışı pekiştiriyor görünse de, özellikle Valensiya ve Granada gibi belirli bölgelerde ciddi ekonomik ve demografik sorunlara yol açtı.
Halktan uzak bir yaşam süren ve pahalı saray eğlencelerine düşkün olan Felipe, giderek büyüyen ekonomik sorunlarla ilgilenmeyerek, bu sorunların sonraki hükümdarların döneminde bir bunalıma dönüşmesinde önemli rol oynadı. Hükümdarlığının ilk yıllarında masrafları kısmak amacıyla sarayın Valladolid’e taşınması (1601-1607), Castilla’daki iktisadi bunalım ve ilk devalüasyonlar yüzünden artan iktisadi ve mali sorunları çözümlemeye yetmedi. Daha sonra sarayını Madrid’e taşıdı.
Kralın, insancıl bir tutumla, Amerikalı yerlilere bir seçim hakkı tanıyarak isterlerse özgür olacaklarını, isterlerse encomienda’da ya da kentte çalışabileceklerini ilan etmesi İspanyol Amerikası’nın çökmesine yol açtı ve Felipe kararından vazgeçmek zorunda kaldı. 1603’te, I. Elizabeth’in yerine I. James’in geçmesi üzerine 1604’te İngiltere ile bir barış antlaşması imzalandı. Hollanda’da, Kalvenistler, Dunes (ya da Nieuwpoort) Savaşı’nı kazandılar (1600), ama mali durumu bozuk olan İspanya savaşa devam edemedi. 1609’da Birleşik Eyaletler’in bağımsızlığını fiilen tanıyan On İki Yıl Ateşkesi imzalandı.
1619’da Portekiz’e yaptığı bir gezinin ardından hastalandı ve iki yıl sonra da öldü.
III. Felipe Altın Post Nişanı sahibiydi.
Döneminde sanat
Dönemindeki güçlüklere karşılık, İspanya o dönemde, özellikle Miguel de Cervantes’in Don Kişot (1605-1615) ve Mateo Alemán’ın Guzman de Alfarache romanlarıyla edebi yaşamının altın çağını yaşıyordu. Diego Velázquez ve Juan Pantoja de la Cruz, kralın birçok portesini çizdiler (Madrid ve Viyana), Giambologna ve Pietro Tacca’nın yaptığı at üstünde heykeliyse Madrid’deki Plaza Mayor’dadır.
- 1631 – John Donne, İngiliz şair (d. 1572)
- 1671 – Anne Hyde, York Dükü James’in (daha sonra Kral II. James) ilk karısı olarak York ve Albany Düşesi (d. 1637)
| Anne Hyde | |
|---|---|
| York ve Albany Düşesi | |

Anne Hyde, 1662
|
|
| Doğum | 12 Mart 1637 Windsor, Berkshire, İngiltere |
| Ölüm | 31 Mart 1671 (34 yaşında) Saint James Sarayı, Westminster, Middlesex |
| Defin | 5 Nisan 1671 Westminster Abbey |
| Eş(ler)i |
II. James (e. 1660)
|
| Babası | Edward Hyde |
| Annesi | Frances Aylesbury |
| Dini | Katolik öncesi. Anglikan |
Anne Hyde (12 Mart 1637 – 31 Mart 1671) York Dükü James’in (daha sonra Kral II. James) ilk karısı olarak York ve Albany Düşesi idi.
Anne, halktan birinin kızıydı – Edward Hyde (daha sonra Clarendon Kontu oldu) ve müstakbel kocasıyla ikisi de Hollanda’da sürgünde yaşarken tanıştı. 1660’ta James ile evlendi ve iki ay sonra çiftin evlilik dışı ilişkiyle dünyaya gelen ilk çocuğunu doğurdu. Bazı gözlemciler evliliği onaylamadı, ancak James’in kardeşi İngiltere kralı II. Charles, evliliğin gerçekleşmesini istedi. Onaylanmamanın bir başka nedeni de, James’in Anne’ye karşı gösterdiği, öpüşme ve birbirine yakın davranma gibi on yedinci yüzyılda halk arasında uygunsuz davranış olarak görülen sevgi gösterileriydi. James ve Anne’nin sekiz çocuğu vardı, ancak altısı erken çocukluk döneminde öldü. Yetişkinliğe kadar hayatta kalan iki çocuğu, geleceğin hükümdarları olan II. Mary ve Anne idi. James, birçok gayri meşru çocuk sahibi olduğu pek çok metresi olan bir çapkındı.
Aslen bir Anglikan olan Anne, James ile evlendikten kısa bir süre sonra Katolikliğe geçti. Hollanda ve Fransa’ya yaptığı ziyaretler sırasında Katoliklik ile tanışmış ve bundan çok etkilenmişti. Kısmen Anne’nin etkisi nedeniyle, James daha sonra Katolikliğe dönüştü ve bu da sonunda Şanlı Devrim’e yol açtı. İlerlemiş meme kanserinden muzdaripti ve son çocuğunu doğurduktan kısa bir süre sonra öldü.
İlk yılları (1637-60)
1629’da Edward Hyde, ilk karısı Grittenham’lı Anne Ayliffe ile evlendi. Evliliğinden altı ay sonra Anne çiçek hastalığına yakalandı, düşük yaptı ve öldü. Üç yıl sonra Hyde, Frances Aylesbury ile evlendi. Çiftin en büyük kızı, 1637’de Windsor’daki Cranbourne Lodge’da [1] doğdu ve Edward Hyde’ın ilk karısının adını (Anne) aldı. Ailesi, tahttan indirilen Kral I. Charles’ın idamından sonra ailesinin Hollanda’ya kaçtı ve 1649’dan önceki hayatı hakkında neredeyse hiçbir şey bilinmiyor.
Birinci İngiliz İç Savaşı sırasında, babası I. Charles’ın önde gelen danışmanıydı, ardından 1646’da oğlu II. Charles ile sürgüne gitti. Birçok mülteci gibi, onlar da Orange’lı Mary’nin birçok İngiliz kaçağa barınak sunduğu Breda’ya yerleşti. Mary, Hyde’dan nefret eden annesi Henrietta Maria’nın isteklerine karşı, Anne’yi nedime olarak atadı.
Anne, Lahey’de ya da Orange Prensesi’nin Teylingen’deki kır evinde tanıştığı insanların genel gözdesi oldu. Çok çekici ve tarz sahibiydi ve birçok erkeği cezbetti. Anne’ye aşık olan ilk erkeklerden biri, Northampton Kontu’nun oğlu Spencer Compton’du. Ancak Anne, hislerine karşılık veren Henry Jermyn’e çabucak aşık oldu. Anne, görevden alınan kralın oğlu York dükü James ile tanıştığında Jermyn’i aynı hızla unuttu. 24 Kasım 1659’da, veya üç yıl sonra, James, kızını odaya kapatan ve iddiaya göre Charles’ı kızını idam etmesi konusunda konuşan babası da dahil olmak üzere birçok kişinin muhalefetine rağmen Anne ile evleneceğine söz verdi. Charles, Anne’nin güçlü karakterinin zayıf iradeli kardeşi üzerinde olumlu bir etkisi olacağını öne sürerek bu tavsiyeyi reddetti.
York Düşesi (1660-1671)
Evlilik

Anne gözle görülür bir şekilde hamileydi ve çift evlenmek zorunda kaldı. Monarşinin Mayıs 1660’taki Restorasyonundan sonra, 3 Eylül 1660’ta Londra’da resmi ama özel bir evlilik töreni düzenlediler. Düğün, Worcester House’da gece 11 ile sabah 2 arasında gerçekleşti. – babasının Strand’daki evi – ve James’in papazı Dr. Joseph Crowther tarafından törenle kutlandı. Fransız Büyükelçisi Anne’yi “neredeyse bir kralın soyuna layık cesaret, zeka ve enerjiye” sahip olarak nitelendirdi.
Çiftin ilk çocuğu Charles o yılın Ekim ayında doğdu, ancak yedi ay sonra öldü. Onu yedi çocuk izledi: Mary (1662-1694), James (1663-1667), Anne (1665-1714), Charles (1666-1667), Edgar (1667-1671), Henrietta (1669-1669) ve Catherine (1671 –1671). Oğullarının hepsi ve iki kızı bebekken öldü.
Evliliklerinden çok sonra bile, bazı gözlemciler, önceden ne söz vermiş olursa olsun, prensin kararını onaylamadılar. Samuel Pepys evlilik hakkında şunları söyledi: “… York Dükü’nün onunla evliliği, başka türlü sıradan bir adam olacak olan Şansölye’yi ulaşılmaz kılarak krallığı alt üst etti. . . .” Anne’nin ölümünden sonra, kraliyet sarayı James için yeni bir eş bulmaya çalıştı, ancak bu yeni eş hiçbir koşulda Anne gibi mütevazı bir soydan değildi. Pepys, James’i tasvir ettiği kadar iyi bir baba olsa da, Anne ve James’in ilk doğan oğullarının ölümünden etkilenmediklerini garip bir şekilde belirtti.[11] Pepys ayrıca Anne’yi “sadece dünyanın en gururlu kadını değil, aynı zamanda en masraflı kadını” olarak nitelendirdi. James’in yeğeni (daha sonra Anne’nin damadı olacak), Orange’lı III. William ve kocasının kuzeni Hanoverli Sophia’nın zihninde bile Hyde’ın halktan gelen soyunun damgası kaldı.
Ev hayatı

Anne, kayınbiraderi tarafından çok sevilmesine rağmen sarayda popüler değildi. “Zamanının en savunmasız avcısı” olarak kabul edilen James’in evlilikleri boyunca art arda metresleri oldu. Aralarında Fransız ordusunda oldukça başarılı bir kariyere sahip olan gayri meşru oğlu Berwick Dükü’nün annesi Arabella Churchill de vardı, James ise kardeşi John Churchill için bir dizi pozisyon aldı.
Anne, kocasının sadakatsizliklerinden habersiz değildi, Pepys kıskandığını ve James’i azarladığını kaydetti, ancak aynı zamanda çiftin sevgilerini halka açık bir şekilde göstermeleri, öpüşmeleri ve birbirleriyle yakınlaşmaları ile ünlü olduklarını iddia etti. Pepys başka bir yazıda James, Lady Chesterfield’a aşık olduğunda, Anne, Charles’a o kadar ısrarlı bir şekilde şikayet etti ki Lady Chesterfield, ölene kadar kaldığı kırsal bölgeye geri çekilmek zorunda kaldığını belirtti.
Tarihçi John Callow, James’in Katolik olmasına yol açan süreçte Anne’nin “en büyük etkiyi yarattığını” iddia ediyor. Katolikliğin biçimleri ve uygulamalarıyla yakından bağlantılı olan Anglikan Yüksek kilise geleneğinde yetişen Anne, 1669’da Anglikan hizmetine katılmayı bıraktı. James, aynı zamanda, ancak Charles’ın isteği üzerine, duyuruyu 1673’e kadar erteledi. [4] Daha sonra Charles’ın kendisi de ölüm döşeğindeyken Katolikliğe geçmesine rağmen, Charles, siyasi nedenlerle çocuklarının Protestan olarak yetiştirilmesinde ısrar etti, bu nedenle hem Mary hem de Anne İngiltere Kilisesi’nin üyeleriydi.
Ölümü

Anne, en küçük oğlu Edgar’ın doğumundan sonraki 15 ay boyunca hastaydı. 1669’da Henrietta’yı ve 1671’de Catherine’i doğurdu. Anne, Catherine’in doğumundan sonra asla düzelmedi. Göğüs kanseri hastasıydı, ve 31 Mart 1671’de öldü. Ölüm döşeğinde, kardeşleri Henry ve Laurence, ona komünyon vermesi için bir Anglikan rahibi getirmeye çalıştı, ancak Anne reddetti. ve Katolik Kilisesi’nin viaticum’unu aldı. Ölümünden iki gün sonra, mumyalanmış bedeni, Westminster Abbey’in Henry VII Şapeli’ndeki İskoç Kraliçesi Mary’nin kasasına defnedildi. Haziran 1671’de Anne’nin hayatta kalan tek oğlu Edgar eceliyle öldü, ardından Aralık’ta Catherine de öldü ve Mary ve Anne’yi York Dükü’nün varisleri olarak bıraktı.
Anne Hyde’ın ölümünden sonra, Willem Wissing tarafından yapılmış bir portresi müstakbel Kraliçe II. Mary tarafından görevlendirildi; bu portre Bu, Windsor Kalesi’ndeki Bahçe Evi’nin Kraliçe’nin Çizim Odası’nın kapısının üzerinde asılıydı. İlk karısının ölümünden iki yıl sonra James, James’in yetişkinliğe kadar hayatta kalan tek oğlu James Francis Edward’ı doğuran Katolik bir prenses olan Modenalı Mary ile evlendi. James, 1685’te İngiltere, İrlanda ve İskoçya’nın kralı oldu , ancak 1688’deki Şanlı Devrim sırasında tahttan indirildi. Taht daha sonra Parlamento tarafından Anne’nin en büyük kızı Mary ve kocası Orange’lı William III’e teklif edildi. [17] Mary 1694’te ve William 1702’de öldükten sonra, Anne Hyde’ın hayatta kalan tek çocuğu Anne, üç krallığın kraliçesi oldu ve 1707’de Birleşik Büyük Britanya Krallığı’nın ilk hükümdarı oldu.
Medya tasvirleri
- 2003 yapımı Charles II: The Power and The Passion (veya The Last King) mini dizisinde Anne Hyde’ı Tabitha Wady canlandırdı.
- 1727 – Isaac Newton, İngiliz matematikçi ve fizikçi (d. 1643)
Isaac Newton
|
Sir
Isaac Newton
|
|
|---|---|

Isaac Newton portresi, 1689
|
|
| Doğum | 4 Ocak 1643 Woolsthorpe, Lincolnshire, İngiltere Krallığı |
| Ölüm | 31 Mart 1727 (84 yaşında) Kensington, Londra, Büyük Britanya Krallığı |
| Defin yeri | Westminster Abbey, İngiltere |
| Milliyet | İngiliz |
| Vatandaşlık | |
| Mezun olduğu okul(lar) | Trinity College, Cambridge, İngiltere |
| Tanınma nedeni | Evrensel kütleçekim yasası Üç hareket yasası |
| Kariyeri | |
| Dalı | Fizik, matematik, din, astronomi, teoloji, felsefe, simya |
| Çalıştığı kurumlar | Cambridge Üniversitesi Royal Society Kraliyet Darphanesi |
| Etkilendikleri | Aristoteles, Bîrûnî, İbn Meymun, Galileo Galilei, Johannes Kepler |
| Etkiledikleri | Voltaire, Edmond Halley, James Clerk Maxwell, David Hume, Immanuel Kant, Albert Einstein, Isaac Asimov |
| İmza | |
|
|
|
|
Amerikalı astrofizikçi ve yazar Michael H. Hart’ın 1978’de yayımladığı “Dünya Tarihine Yön Veren En Etkili 100 (The 100: A Ranking of the Most Influential Persons in History)” adlı kitabında Isaac Newton, İslam peygamberi Muhammed’den sonra 2. sırada yer alarak diğer bilim insanlarının en üstünde yer almıştır.
|
|
Isaac Newton (d. 4 Ocak 1643, Woolsthorpe-by-Colsterworth – ö. 31 Mart 1727, Kensington), İngiliz fizikçi, matematikçi, astronom, mucit, simyacı, teolog ve filozoftur. 1687 yılında yayımladığı Philosophiæ Naturalis Principia Mathematica (Doğa Felsefesinin Matematiksel İlkeleri) kitabıyla klasik fizik mekaniğinin temelini oluşturmuş ve bu eser, dünya tarihinin en önemli bilimsel kitaplarından biri olmuştur. Bu eserle birlikte kendi adıyla anılan evrensel kütleçekim yasası ve üç hareket yasasını ortaya koymuş ve kendisinin yaratmış olduğu bu etki, bilim tarihindeki kilometre taşlarından biri olmuştur. Newton’ın evrensel kütleçekimi ve hareketin üç kanunu, sonraki üç yüzyıl boyunca bilim dünyasına egemen olmuştur.
Newton, dünyadaki nesnelerin hareketleri ile gökyüzündeki nesnelerin hareketlerinin aynı doğal yasalar ile yönetildiklerini kendi kütleçekim kanunu ve Alman gök bilimci Johannes Kepler’in gezegen hareketleri kanunu arasındaki tutarlılıklar ile göstermiştir. Newton aynı zamanda ilk yansıtmalı teleskobu geliştirmiş, beyaz ışığın bir prizmaya tutulduğunda farklı renklerden bir tayf yapması gözlemi sonucu bir renk kuramı da oluşturmuştur.
Isaac Newton, günümüz bilim insanları tarafından bilim tarihinin en etkili insanlarından biri olarak kabul edilmektedir. 1999 yılının sonlarında, 100 ileri gelen fizikçiyle gerçekleştirilen milenyum oylamasında Isaac Newton, tüm zamanların en iyi fizikçileri arasında Albert Einstein’dan sonra 2. sırayı almıştır. Amerikalı astrofizikçi ve yazar Michael H. Hart’ın 1978 yılında yayımladığı Dünyaya Yön Veren En Etkin 100 Kişi adlı kitabında ise Newton, 2. sırada yer alarak Albert Einstein dahil tüm bilim insanlarının üstünde tutulmuştur. Ünlü bilimkurgu yazarı Isaac Asimov da, Newton’dan ”tarihin en büyük bilim insanı” olarak bahsetmiştir.
Hayatı
İlk yılları (1643-1661)

24 Aralık 1642’de (Gregoryen Takvimine göre 3 Ocak 1643) annesi Hannah’ın doğum sancıları başladı. Gece yarısından bir veya iki saat sonra da, Noel sabahında, 25 Aralık 1642 tarihinde (Gregoryen Takvimine göre 4 Ocak 1643), İngiltere’nin Grantham şehrinin yakınlarındaki Woolsthorpe’da bir erken doğum sonucu bebek Newton dünyaya geldi. Newton oldukça zayıf bir çocuktu ve hatta ilk günlerinde hayatta kalacağı beklenmiyordu. Adını, doğumundan üç ay önce ölen ve zengin bir çiftçi olan babasından almıştı.
Isaac adı, İncil ve Kur’an’da İshak (İsḥāq) adıyla geçen peygamberden gelmektedir. İnanca göre Tanrı, çocuklarının olacağını müjdelemesi üzerine, çok ileri yaşta olan İbrahim Peygamber ve o güne kadar hiç çocuğu olmamış olan eşi Sâre, bu müjdeye gülmüşlerdi. Bu nedenle Tanrı, çocuğun adının İshak (Isaac), yani ”gülmek” anlamına gelen bir sözcük olması gerektiğini buyurdu.
Newton henüz 4 yaşındayken, annesi zengin bir din adamıyla evlendi ve yeni kocasının yanına yerleşti. Annesi Newton’ı anneannesine bıraktı ve Newton yedi yıl anneannesinin yanında kaldı. Bu travmatik durum, Newton’ın, ailesinden ve özellikle de üvey babasından nefret etmesine neden oldu. Newton, 12 yaşından 17 yaşına kadar bir eczacı olan William’ın evinde yaşadı ve burada hem simyaya hem de eczacının üvey kızı Miss Storey’den etkilenmeye başladı.
Annesi, kocası yedi yıl sonra ölünce, kendisine oldukça yüklü bir miras kalarak geri döndü. 12 yaşında Grantham’da King’s School’da (Kralın Okulu) eğitime başladı ve 1661’de bitirdi. Bir dönem annesi onu çiftçi yapmak için okuldan aldı, ama Newton çiftlik işlerine hiç ilgi duymuyordu. Annesi Newton’ı çiftlik işleri ile uğraşıyor zannederken, Newton aslında sürekli gökyüzünü ve yıldızları inceliyor, kitaplar okuyor ve çeşitli notlar alıyordu. En sonunda annesini okula gitmesi ve üniversiteye hazırlanması gerektiğine ikna etti ve okula geri döndü.
19 yaşındayken, eczacı William’ın üvey kızı Miss Storey ile nişanlanmış, fakat Newton’ın yoğun dersleri nedeniyle ilişkileri sonlanmıştır.[17] Newton daha sonradan, hayatı boyunca hiç evlenmedi ve kendisinin başka bir ilişkisi de bilinmemektedir; sadece bu ilişkiyi hep hatırladığı söylenir.
Cambridge’deki yılları (1661-1665)
Newton, 1661 yılında Cambridge’de Trinity College’a girdi. Okula “sizar” olarak girmişti, yani hem okulda çalışıyor hem de okuyordu. Cambridge’de Copernicus ve Kepler’in teorileri göz ardı ediliyor, Galileo’nun çalışmaları tanınmıyordu ve ortama Aristoteles felsefesi hâkimdi. Newton burada üç yıl boyunca cebir, geometri ve trigonometri dersleri aldı, Latince ve Antik Yunancayı öğrendi. Ayrıca bu dönemde Galileo ve Kepler’in eserleri ile tanıştı ve oldukça etkilendi. Descartes, Gassendi, Hobbes ve özellikle Boyle’un felsefi çalışmalarını da okudu.
Newton, fikirlerini yazdığı Quaestiones Quaedam Philosophicae (Bazı Felsefi Sorular) adlı defterinin başına Latince şu notu düşmüştür:
“Platon arkadaşım, Aristoteles arkadaşım, ama en iyi arkadaşım gerçek.”
Newton, Cambridge’de geçirdiği yıllarda diğer öğrenciler arasında başarılı olarak sıyrılamamıştı ve dâhiliğini, ortaya çıkan veba salgını nedeniyle kendi çiftliğinde geçirdiği iki yılda göstermişti.
Çiftlikteki çalışmaları (1665-1667)


1665 yılının Ağustos ayında Londra’da başlayan veba salgını nedeniyle Cambridge’deki Trinity College kapatıldı ve Newton, 1667’nin Mart ayına kadar Woolsthorpe kasabasındaki çiftliğinde kaldı. Çiftlikte geçirdiği bu iki sene oldukça verimliydi ve bu dönemde kütleçekim üzerinde düşünmeye başladı. Çiftlikteki çalışmalarında diferansiyel ve integral hesaplamalarının da temelini attı. Geçmişte alan, yay uzunluğu, tanjant bulma gibi eskiden kullanılan yöntemleri diferansiyel hesaplamayı temel alarak birleştirdi. Çiftlikte karanlık bir odada güneş ışığını bir prizmaya tutarak ışık tayfı oluşturmuş ve beyaz ışığın tek başına bir birim olmadığını fark etmiştir.
Cambridge’e dönüşü (1667-1696)
1667 yılında Newton, üniversite tekrar açılınca Cambridge’e geri döndü ve iki yıl sonra matematik profesörü oldu. Yaklaşık 30 yıl Cambridge’de kaldı, mektuplar yoluyla diğer bilim insanları ile konuşarak tek başına çalışmalarına devam etti. Bu yıllarda, en büyük eseri olan Principia kitabını hazırladı ve tamamladı. Işık ile ilgili çiftliğinde yaptığı deneyler sonucu mercekli teleskopların kusurlar yarattığını fark etti ve bunun üzerine kendisi bir yansıtmalı teleskop geliştirdi. 1668 yılında bu teleskop ile bilim dünyasının ilgisini çekti ve 1672 yılında da Royal Society’nin üyesi oldu.
Principia (1687)

Isaac Newton, dünya tarihinin en önemli bilim eserlerinden biri olan Philosophiæ Naturalis Principia Mathematica (Doğa Felsefesinin Matematiksel İlkeleri) kitabını Latince olarak yayımladı. Kitapta ispatları geometri ile yapmış, evrensel kütleçekim yasasını açıklamış ve cisimlerin kütleleri ile doğru, mesafeleri ile de ters orantılı olarak birbirlerini çektiklerini açıklamıştır.
Kitap, Newton tarafından üç ana bölüme ayrılmıştır. Birinci bölümde Galileo’nun deneylerinden övgü ile söz eder ve Kepler kanunlarını matematiksel olarak ispatlar. Bu bölümde kendi ismi ile anılan ”Newton hareket yasalarını” açıklamıştır. İkinci bölümde de, akışkan içindeki hareketleri incelemiştir ve en iyi gemi tasarımı için öneriler koymuştur. Bu bölümde dalga hareketlerini matematiksel incelemesi ilgi çekmiştir.
Londra’daki yılları ve ölümü (1696-1727)

1696’da Newton’a Kraliyet Darphanesi’nin müdürlüğü teklif edildi ve Newton bunu kabul ederek Londra’ya yerleşti. Bu işini çok ciddiye almıştı ve özellikle sahte paralara karşı büyük bir mücadele başlattı. Newton, Londra’daki yaşamı sevmişti ve artık akademik çalışmalar ile çok ilgilenmek istemiyordu. 1703’te Royal Society’nin başına getirildi ve ölümüne kadar bu görevde kaldı. 1705’te şövalyelik unvanı aldı. 1706’da kraliyet derneğinin başkanlığına seçildi. 1708’de Kraliçe Anne tarafından “Sir” unvanıyla ödüllendirildi.
Isaac Newton, 31 Mart 1727 tarihinde, 84 yaşındayken öldü ve Westminster Manastırı’na gömüldü.
Opticks (1704)
1704’te ışık ve renkleri konu alan The Opticks kitabını yayımladı.[21] Kitabını Principia‘da olduğu gibi Latince değil, İngilizce basmıştı. Böylece Newton, kitabı aracılığıyla daha geniş kitlelere ulaşabilmiştir. Kitapta yansıma ve kırınım hesapları, beyaz ışığın tayfın renklerine ayrılması, gözün çalışma yöntemi, merceklerle görüntü oluşumu, gökkuşağının renkleri, yansıma, teleskopun yapımı gibi konulardan bahseder.
Newton’ın büyük bir eleştirilme ve yadırganma korkusu vardı; bu nedenle buluşlarını ilk düşündükten yıllar sonra yayımladığı düşünülmektedir. Bu yönü, bazı bilim insanları ile sert tartışmalara girmesine de neden olmuştur. Leibniz’i kendi fikirlerini çalmak ile suçlamış, ününü ve gücünü kullanarak Leibniz’in kendisini savunmasına engel olmaya çalışmıştır. Başka bir fizikçi Robert Hooke ile çeşitli konularda tartışmaları olmuştur. Newton’ın, Principia kitabını yayımlamak için Hooke’un ölümü beklediği de söylenir; çünkü kitap Hooke’un ölümünden bir sene sonra yayımlanmıştır.
Bilimsel yöntemi

Newton, Principia kitabının giriş kısmında bilimin olması gereken amacını şu şekilde belirtmiştir:
Olgulardan doğanın kuvvetlerini keşfetmek, sonra da bu kuvvetler yardımıyla diğer olayları açıklamak…
Ona göre önce olgular gözlemlenmeli, bu gözlemler sonucu doğanın yasaları keşfedilmeli ve sonrasında oluşturulan kuram, bu olayları açıklayabilmelidir.
Newton’a göre doğa, matematiksel niteliklere sahip bölünemez küçük parçacıklardan yapılmıştır ve doğada her olay bu parçacıkların birleşmesi ve dağılması ile oluşmuştur. Ona göre bilimin amacı, deneyler ile birlikte bu olayları matematiksel kuramlar ile genelleştirmektir.
Bilimsel çalışmaları
Matematik
Newton’un matematikte neredeyse her dalda katkıları olmuştur. Özellikle analitik geometride eğrilerin teğetleri (diferansiyel) ve eğrilerin oluşturduğu alanları (integral) hesaplamada yöntemler geliştirmiştir. Bu iki işlemin birbirlerine ters olduğunu bulmuş, eğimler ile ilgili çözümler geliştirmiş ve bunlara akış (fluxion) metotları ismini vermiştir çünkü niceliklerin bir boyuttan diğerine aktığını hayal etmiştir.
Matematikte (a+b)n ifadesinin üstel seriye açılımını veren genel iki terimli teoremini buldu.
Leibniz ile kalkülüs tartışması
Newton, “akış” yöntemlerini 1666 yılında geliştirmişti ve sadece birkaç matematikçiye özel olarak göstermişti. 1675’te Paris’te Gottfried Wilhelm Leibniz de tamamen bağımsız olarak kendi diferansiyel yöntemini geliştirdi. Leibniz 1684’te kendi yöntemini yayınlayınca, bilim dünyasında bu yöntemi önce kimin bulduğuna dair sert bir tartışma başladı ve 1716’da Leibniz öldükten sonra bile tartışma devam etti. Günümüzde tarihçiler Newton ve Leibniz’in birbirlerinden tamamen habersiz bu yöntemleri geliştirdiklerini düşünüyorlar.
Mekanik
Newton’un bilime en büyük katkısı mekanik alanındadır. Merkezkaç kuvveti yasası ile Kepler yasalarını birlikte ele alarak kütleçekim yasasını ortaya koydu. Newton hareket yasaları olarak bilinen eylemsizlik ilkesi, kuvvetin kütle ile ivmenin çarpımına eşit olduğunu ifade eden yasa ve etki ile tepkinin eşitliği fiziğin en önemli yasalarındandır.

Kütle çekimi
Newton denilince akla ilk kütleçekim gelir çünkü fizik tarihinde bu fikir bir devrim yaratmıştır. Newton’dan önce Joannes Kepler, gezegenlerin eliptik hareketlerini salt matematiksel olarak açıklamıştı ama gezegenlerin neden yörüngede kaldıklarına dair bir açıklama getirmemişti.
Newton kütleçekimi ilk kez 1665 yılında düşündü ama Principia kitabını 1687 tarihine kadar yayınlamadı.
Newton öncelikle Kepler yasalarının doğru olması durumunda Güneş ve gezegenler arasında bir çekim kuvveti olması gerektiğini düşündü. Bu tür bir kuvvet olması durumunda gezegenlerin Kepler’in tarif ettiği şekilde hareket edeceğini düşündü ve kütleçekimin matematiksel ifadesini verdi.
Formülleri
F=Gm1m2d2
-
- *G=0.0000000000667 (N∗m2kg2)
- *m1=birinci nesnenin kütlesi (kg)
- *m2=ikinci nesnenin kütlesi (kg)
- *d=aralarındaki uzaklık (m)
- *F=Kuvvet (Newton [N])
F=ma
-
- *F=Kuvvet (Newton [N])
- *m=kütle (kg)
- *a=ivme (msn2)
Newton mekaniği
Newton mekaniği yakın çevremizdeki hareketleri açıklayan bir bakış açısıdır, atom altı parçacıkları için kuantum mekaniği, galaktik hareketler için ise görelilik kuramları uygulanır. Newton mekaniği büyük yıldız ve gezegenlerin yörüngelerini hesaplarken bazı küçük sapmalara neden olmaktadır fakat dünyadaki küçük cisimler ve mühendislik hesaplamalarında bunlar tamamen göz ardı edilebilecek kadar küçüktür.
Newton hareket yasaları
Newton hareket yasaları olarak bilinen üç yasa şu şekildedir:
- Hareketli bir cisim dışarıdan bir kuvvete maruz kalmazsa doğrusal hareketini sürdürür.
- Bir cismin kütlesi ne kadar fazla ise hareket ettirici bir etkiye direnci o kadar büyük olur. (F=ma)
- Her etkiye karşı ona eşit ve karşıt yönde bir tepki vardır.
Newton’un hareket yasaları, evrenin bir düzen içinde ve deterministik olduğu sonucuna varmış ve sonrasında felsefeyi oldukça etkilemiştir.

Optik
Newton bir ışık kaynağından çıkan ışığın bir cisme çarpıp aydınlatması olayına farklı bakmış, ışığın hareket ettiğini ve sonlu bir hızı olduğunu düşünmüştür. Mercek ve prizmalar kullanarak bu ışık tayfını tekrar beyaz ışığa çevirmeyi de başarmıştır.
Newton karanlık bir odada küçük bir delikten gelen güneş ışığını bir prizmadan geçirerek bir renk tayfı oluşturmuş ve gökkuşaklarının nasıl oluştuğunu açıklamıştır.
Başlıca eserleri
- Method
- De Motu Corporum in Gyrum (1684)
- Philosophiae Naturalis Principia Mathematica (1687)
- Opticks (1704)
- Arithmetica Universalis (1707)
- The System of the World, Optical Lectures, The Chronology of Ancient Kingdoms, (Amended)5 Kasım 2008 tarihinde Wayback Machine sitesinde arşivlendi. and De mundi systemate (published posthumously in 1728)
- ObservationsProphecies Of Daniel and Apocalypse of St. John (1733)
- An Historical Account of Two Notable Corruptions of Scripture(1754)
Ayrıca bakınız
Newton’un hareket yasaları

Newton’un hareket yasaları, bir cisim üzerine etki eden kuvvetler ve cismin yaptığı hareket arasındaki ilişkileri ortaya koyan üç yasadır. İlk kez Isaac Newton tarafından 5 Temmuz 1687 tarihinde yayımlanan Philosophiae Naturalis Principia Mathematica adlı çalışmada ortaya konmuştur. Bu yasalar klasik mekaniğin temelini oluşturmuş, bizzat Newton tarafından fiziksel nesnelerin hareketleri ile ilgili birçok olayın açıklanmasında kullanılmıştır. Newton, çalışmasının üçüncü bölümünde, bu hareket yasalarını ve yine kendi bulduğu evrensel kütleçekim yasasını kullanarak Kepler’in gezegensel hareket yasalarının elde edilebileceğini göstermiştir.
- 1. Yasa
- Eylemsiz referans sistemi adı verilen öyle referans sistemleri seçebiliriz ki, bu sistemde bulunan bir parçacık üzerine bir net kuvvet etki etmiyorsa cismin hızında herhangi bir değişiklik olmaz. Bu yasa genellikle şu şekilde basitleştirilir: “Bir cisim üzerine dengelenmemiş bir dış kuvvet etki etmedikçe, cisim hareket durumunu (durağanlık veya sabit hızlı hareket) korur.”
- 2. Yasa
- Eylemsiz bir referans sisteminde, bir parçacık üzerindeki net kuvvet onun çizgisel momentumunun zaman ile değişimi ile orantılıdır:
- F=m⋅dvdt
Momentum (mv), kütle ile hızın çarpımına eşittir. Kuvvet ve momentum vektörel nicelikler olduğundan, net kuvvet cisim üzerine etki eden tüm kuvvetlerin vektörel toplamı ile bulunur. Bu yasa sıklıkla şu şekilde ifade edilir: “F=ma: Bir cisim üzerindeki net kuvvet, cismin kütlesi ile ivmesinin çarpımına eşittir.”
- 3. Yasa
- Bir cisme, bir kuvvet etki ediyorsa; cisimden kuvvete doğru eşit büyüklükte ve zıt yönde bir tepki kuvveti oluşur. Burada dikkat edilmesi gereken bu kuvvetlerin aynı doğrultu üzerinde olduğudur. Bu yasa çoğu zaman şu cümle ile basitleştirilebilir: “Her etkiye karşılık eşit büyüklükte ve zıt bir tepki vardır.”
Bu yasalara getirilen çeşitli yorumlar vardır. En genel olan yorumda kütle, ivme ve (en önemlisi) kuvvetin önceden tanımlanmış olduğu varsayılmaktadır. Ancak Newton’ın birinci ve ikinci yasasının aslında kuvvetin ve kütlenin tanımı olduğuna dair yorumlar da mevcuttur.
Dikkat edilirse ikinci yasa ancak gözlem bir eylemsiz referans sisteminden yapıldığında geçerlidir. Eylemsiz referans sistemi birinci yasada tanımlanmış olduğundan ikinci yasayı kullanarak birinci yasanın ispatını aramak mantıksal bir yanılgı olacaktır.
Işık hızına yaklaşan hızlarda Newton yasaları fiziksel olayları açıklamakta yetersiz kalmakta, bu nedenle geçerliliklerini yitirmektedirler. Işık hızlarına yakın hızlarda cisimlerin hareketi incelenirken Albert Einstein’ın geliştirdiği özel görelilik teorisi dikkate alınmalıdır.
Newton’un hareket kanunları
Newton’un birinci yasası: Eylemsizlik yasası
| “ | Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare. | „ |
| “ | Yasa I: Tüm cisimler bir kuvvet etkisi tarafından durumunu değiştirmeye zorlanmadıkça düzgün doğrusal hareketini veya durağanlığını korur. | „ |
Basitleştirilmiş bir şekilde, bir cisim üzerindeki net kuvvet, o cisim üzerine etki eden tüm kuvvetlerin vektörel toplamıdır. Bu toplam sıfır ise, Newton’ın birinci yasası cismin hareket durumunun değişmeyeceğini söyler. Aslında burada iki durum oluşur:
- Hareket etmeyen bir cisim, üzerine bir net kuvvet etki edinceye dek hareket etmeyecektir.
- Hareketli bir cisim, üzerine net bir kuvvet etki etmedikçe hızını değiştirmeyecektir (ivmelenmeyecektir).
Birinci durum çoğu kişi tarafından açıkça anlaşılabilir olmasına rağmen, ikinci durumu anlamak için üzerinde biraz düşünmek gereklidir çünkü gündelik yaşantımızda hareketini sürekli olarak sürdüren cisimleri pek görmeyiz (göksel hareketler hariç). Bir kalemi masa üzerinde kaydırırsak, hareketini sonsuza dek sürdürmeyecek, yavaşlayıp en sonunda duracaktır. Kalemin hızı değişmiştir ve Newton’ın yasalarına göre böyle bir hız değişikliği ancak cisim üzerine bir net kuvvet etki etmesi sonucunda oluşabilir. Bu kuvvet kalem ve masa arasında, kalemin hareketinin tersi yöndeki sürtünme kuvvetidir ve cismin yavaşlamasına neden olmaktadır. Böyle bir kuvvetin yokluğunda kalemin hızı azalmayacak, hareketini sürdürmeye devam edecektir. Sürtünme kuvvetinin az olduğu durumlara bir örnek olarak bir hava hokeyi masası veya buz pateni pisti verilebilir.
Yasanın doğruluğunu mükemmel bir şekilde gösteren deneyler sürtünmenin her deneyde kaçınılmaz olarak ortaya çıktığı için yapılamamaktadır. Öyle ki dış uzayda bile engellenemeyen kütleçekimsel kuvvetler böylesi mükemmel bir deneyin yapılmasını engellemektedir. Ancak yine de yasa, bir nesnenin hareket durumundaki değişikliğin temel nedenlerini vurgulamakta işe yaramaktadır.
Newton’ın birinci yasası eylemsizlik yasası olarak da bilinmektedir ve sıklıkla “sıfır net kuvvet, sıfır ivmelenmeye karşılık gelir.” şeklinde açıklanır. Ancak bu açıklama fazla basitleştirilmiştir. Newton tarafından formüle edildiği üzere, birinci yasa ikinci yasanın özel bir hali olmaktan daha fazla şey içerir. Newton iyi bir nedenle yasalarını hiyerarşik bir sıralamada düzenlemiştir. Öyle ki birinci yasa, diğer yasaların uygulanabilir olduğu “eylemsiz referans çerçeveleri” olarak adlandırılan referans çerçevelerini tanımlar. Yasaların niçin eylemsiz referans sistemleri ile sınırlı olduğunu anlamak için ivmeli hareket eden bir cisim (örneğin pistte kalkış için hızlanmakta olan bir uçak) içinde duran bir topu göz önüne alın. Uçak içinde bulunan herhangi bir kişinin bakış açısından (ya da teknik bir deyiş ile “uçağın referans çerçevesinden”) uçak ileri doğru ivmelendikçe, top geriye doğru hareket ediyormuş gibi görünecektir (bu etki uçak ivmelenirken sizi koltuğunuza bastıran etki ile aynıdır). Uçak içindeki yolcuların bakış açısından topu hareket ettirecek hiçbir kuvvet bulunmamasına rağmen topun bu hareketi, Newton’ın ikinci yasası ile çelişir gibi görünmektedir. Gerçekte ise ikinci yasa ile ilgili bir çelişki yoktur çünkü Newton’ın ikinci yasası böyle bir durum için uygulanabilir değildir: İkinci yasa ancak topun üzerine bir kuvvet etki etmediğinde onun sabit kalacağı eylemsiz referans sistemlerinde (birinci yasada tanımlanan) geçerlidir. Bu durumda “uçak referans sistemi” bir eylemsiz referans sistemi değildir. Görüldüğü üzere, tüm yasalar her durumda uygulanabilir olmadığından, çeşitli yasaların çeşitli durumlara uygulanabilir olup olmadıkları konusu önem taşımaktadır. Özetlemek gerekirse:
- Eylemsiz referans sistemleri olarak adlandırılan öyle referans sistemleri vardır ki bu sistemlerde bulunan gözlemciler için üzerine herhangi bir kuvvet etki etmeyen tüm cisimler hareket durumunu korur.
Eylemsizlik yasasının tarihi
Newton’ın birinci yasası Galileo tarafından daha önce açıklanan eylemsizlik yasasının bir yeniden ifadesidir. Bu görüş, tüm cisimlerin evrende doğal bir yerinin olduğunu söyleyen Aristocu görüşten farklıdır. Aristo, kayalar gibi ağır cisimlerin Dünya üzerinde, duman gibi hafif nesnelerin gökyüzünde, yıldızların ise cennette durma isteklerinin olduğuna inanıyordu. Buna rağmen Aristo’nun ve Galileo’nun fikirleri arasındaki temel fark Galileo’nun bir cisim üzerine etki eden kuvvetin cismin hızını değil ivmesini belirliyor olduğunu söylemesidir. Yine Aristo’dan farklı olarak Galileo bu söylemini inançlarına değil, deney ve gözleme dayalı olarak ortaya koymuştur. Bu anlayış Newton’ın, birinci yasasını (kuvvet yoksa, ivme yoktur) oluşturmasında yol göstermiş ve üzerine kuvvet etkimeyen cisimlerin hızlarını koruyacağı görüşünü ortaya çıkarmıştır.
Görünüşe göre eylemsizlik yasası birbirinden bağımsız olarak birkaç doğa filozofu tarafından keşfedilmiştir. Hareketin eylemsizliği MÖ 3. yüzyılda Çin filozofu Mo Tzu tarafından, MS. 11. yüzyılda İslam bilginleri İbn-i Heysem ve İbn-i Sina tarafından açıklanmıştır. 17. yüzyılda yaşamış olan filozof René Descartes yasayı formüle etmiştir ancak onu doğrulamak için hiçbir deney yapmamıştır.
Newton’un ikinci yasası: Dinamiğin temel prensibi
| “ | Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.. | „ |
| “ | Yasa II: Bir cismin momentumundaki değişim, cisim üzerine uygulanan itme ile orantılıdır ve itmenin uygulandığı düz doğru boyunca meydana gelir. | „ |
Newton’ın Latince kitabından Motte’nin 1729 yılında yaptığı çeviride ikinci hareket yasası aşağıdaki gibi ifade edilmiştir:
| “ | Hareketin değişimi, uygulanan hareket ettirici kuvvet ile doğru orantılıdır ve kuvvetin uygulandığı düz çizginin doğrultusundadır. -Bir kuvvet ister tümüyle bir seferde, isterse de kademeli ve art arda uygulansın, eğer bir hareket oluşturuyorsa, bu kuvvetin iki katı büyüklüğe sahip başka bir kuvvet hareketi ikiye, üç katı büyüklüğündeki bir kuvvet hareketi üçe katlayacaktır. Ve bu hareket (uygulanan kuvvet ile her zaman aynı doğrultuda), eğer cisim daha önceden hareket halinde ise, önceki hareket ile aynı doğrultuda olması durumunda önceki hareket ile toplanır, önceki hareket ile zıt doğrultuda olması durumunda önceki hareketten çıkartılır. Eğer önceki hareketin doğrultusu ile uygulanan kuvvet etkisi ile oluşturulan yeni hareketin doğrultusu birbirinden farklı ise cismin sonuç olarak hareketi, doğrultuları farklı bu iki hareketin bileşimi şeklinde olacaktır. | „ |
Modern sembolik gösterim ile Newton’ın ikinci yasası bir vektörel diferansiyel denklem şeklinde yazılabilir:
- Fnet=d(mv)dt
Burada F kuvvet, m kütle, v hız vektörü ve t zamandır.
Kütle ve hızın çarpımı cismin momentumu olarak tanımlanmıştır (Newton tarafından bu çarpım “hareket miktarı” olarak adlandırılmıştır). Bu eşitlik sabit kütleye sahip sistemler için kuvvet ve momentum arasındaki fiziksel ilişkiyi ifade eder. Eşitlik sıfır net kuvvet etkisi altındaki bir sistemin momentumunun zamanla değişmeyeceğini söyler. Buna rağmen böyle bir durumdaki sisteme giren veya çıkan herhangi bir miktardaki kütle, bir dış kuvvet etkisi sonucu olmaksızın sistemin momentumunu değiştirecektir ki bu durum ikinci yasaya aykırıdır. Böyle durumlarda bu eşitlik geçersizdir.
Bakınız açık sistemler.
Bu eşitliğin eylemsizlik yasası ile uyumlu olması açısından belirtilmelidir ki, momentumun büyüklüğü değişmeksizin, sadece yönü değişiyorsa, momentumun zamana göre türevi sıfırdan farklı olmalıdır.
Sistemin kütlesi sabit olduğundan bu diferansiyel denklem daha basit ve bilinen bir formda yazılabilir:
- F=ma
Bu eşitlikte
- a=dvdt
ivmeyi belirtmektedir.
F=ma eşitliğini sözlü olarak “bir cismin ivmesi, üzerine uygulanan kuvvet ile doğru, cismin kütlesi ile ters orantılıdır.” şeklinde ifade edebiliriz. Genel olarak, ışık hızına göre düşük olan hızlarda, momentum ve hız arasındaki ilişki yaklaşık olarak doğrusaldır. Gündelik yaşamımızda deneyimlediğimiz neredeyse tüm hızlar bu kategoridedir. Buna rağmen, ışık hızına yaklaşan hızlarda momentum-hız arasındaki bu doğrusal yaklaşım giderek artan biçimde hatalı olmaktadır ve özel görelilik kuramının kullanımına ihtiyaç duyulmaktadır.
İtme
İtme terimi ikinci yasa ile yakından ilişkilidir ve tarihsel olarak yasanın orijinal anlamına daha yakındır. İtme aşağıdaki gibi tanımlanmaktadır:
- Bir itme, bir F kuvvetinin Δt zaman aralığı boyunca etkimesi sonucu oluşur ve ∫ΔtFdt ifadesi ile gösterilir.
Newton tarafından “İtme” kavramı hareket ettirici kuvvet olarak, “Momentum” kavramı ise hareket olarak ifade edilmiştir. Sonuç olarak ikinci yasanın tarihsel yaklaşım ile itme ve momentum değişimi arasındaki ilişkiyi böyle açıkladığı söylenebilir. Dolayısıyla ikinci yasa orijinaline uygun şekilde matematiksel olarak sonlu farklar şeklinde ifade edilebilir:
- I=Δp=mΔv
Burada I itme, Δp momentumdaki değişim, m kütle ve Δv hızdaki değişimdir.
Çarpışmaların analizinde itme kavramı kullanılmaktadır.
Değişken kütleli sistemler
Yaktığı yakıtı püskürterek yol alan ve bir roket gibi değişken kütleli sistemler, kapalı sistem değildirler. Bu tip sistemleri incelerken ikinci yasadaki kütleyi doğrudan zamanın bir fonksiyonu olarak alamayız. Bunun nedeni, Kleppner ve Kolenkow’un An Introduction to Mechanics (Mekaniğe giriş) kitabında ve diğer modern metinlerde verildiği üzere, Newton’ın ikinci yasasının temel olarak noktasal parçacıklara uygulanabilmesidir. Klasik mekanikte parçacıklar, tanımları gereği sabit kütleye sahiptirler. İyi tanımlanmış parçacık sistemleri için Newton yasaları, sistemde bulunan tüm parçacıklar üzerinden toplam alınarak genişletilebilir:
- Fnet=Makm
Burada Fnet sistem üzerindeki toplam dış kuvvet, M sistemin toplam kütlesi ve akm sistemin kütle merkezinin ivmelenmesidir.
Bir roket, su sızdıran bir kova veya ucu salınan şişirilmiş bir balon gibi değişken kütleli sistemleri parçacık sistemleri olarak ele alıp işlem yapmak genellikle çok zordur, bu nedenle bu tip sistemler için Newton’ın ikinci yasası doğrudan uygulanamaz. Bunun yerine m kütlesi zamanla artan veya azalan bir cismin genel hareket denklemi, ikinci yasanın, sisteme giren veya sistemden ayrılan kütle tarafından taşınan momentumu ifade eden bir terimin eklenerek yeniden düzenlenmesiyle elde edilir:
- F+udmdt=mdvdt
Burada u sistemden kaçan veya sisteme giren kütlenin, sistemin kütle merkezine göre hızıdır. Kimi standartlara göre, denklemin sağ tarafında “tepki” (İng. thrust) olarak adlandırılan u dm/dt ifadesi, kuvvet (değişen kütle nedeniyle cisim üzerine uygulanan kuvvet, roket egzozu gibi) olarak tanımlanır ve F niceliğine dahil edilir. İvmenin tanımının da yerine koyulması ile eşitlik,
- F=ma.
halini alır.
Görelilik
- Özel göreliliği göz önüne alarak, bileşke kuvvet yasası ivme cinsinden aşağıdaki gibi ifade edilebilir:
- F=dpdt=d(mv)dt=mdvdt+dmdtv=mdvdt+1c2dEdtv=mdvdt+F⋅vc2v
Bu eşitliğin elde edilmesinde enerjinin meşhur E=mc2 ifadesi kullanılmıştır. (dm/dt=(1/c2)dE/dt) Dikkat edilmesi gereken nokta bu eşitliğin yaklaşık bir eşitlik olduğudur. (Bir cismin toplam enerjisi E=γmc2 olarak ifade edilir. γ Lorentz faktörü olup ışık hızından çok daha yavaş hareket eden cisimler için yaklaşık olarak birdir.) Aşağıdaki eşitlik bir kuvvet tarafından birim zamanda yapılan işi ifade eder:
- dEdt=F⋅v
Burada F·v, vektörel skaler çarpımdır.
Bu denklem genişletilmiş bir kuvvet yasası için tekrar düzenlenebilir:
- mdvdt=F−F⋅vc2v,
Bu eşitlik momentum değişiminin kuvvet doğrultusunda olmasına rağmen, bir kütlenin ivmesinin genel olarak kuvvetin doğrultusunda olmadığını göstermektedir. Buna rağmen eğer hareket eden bir cismin hızı ışık hızından çok düşükse, yukarıdaki eşitlik bilindik F=ma eşitliğine dönüşür.
Açık sistemler
Kütlesi değişen sistemler kapalı sistemler değildir. Örneğin yaktığı yakıtları dışarı püskürterek hareket eden bir roket için, Newton’ın ikinci yasasında kütleyi doğrudan zamanın bir fonksiyonu olarak alarak işe koyulamayız. Bunun nedeni, Kleppner ve Kolenkow ‘un An Introduction to Mechanics adlı kitabında ve diğer modern metinlerde verildiği üzere Newton’ın ikinci yasasının temel olarak sadece parçacıklara uygulanabilir olmasıdır. Klasik mekanikte parçacıklar sabit kütleli olarak tanımlanır. Parçacıklar iyi tanımlanmış sistemleri oluşturduğu takdirde, Newton’ın yasası tüm parçacıklar üzerinden bir toplam alınarak genişletilebilir. Bu durumda sistemi oluşturan tüm parçacıklar kütle merkezinde bulunan, kütlesi tüm parçacıkların kütleleri toplamına eşit bir tek parçacıkmış gibi ele alınabilir. İkinci yasayı böylesi genişletilmiş cisimlere uygularken, yasa tamamıyla cismin iyi tanımlanmış parçacıklardan meydana geldiğini kabul eder. Buna rağmen bir roket gibi değişken kütleli sistemler belli sayıdaki parçacıklardan oluşmaz. Böyle sistemler iyi tanımlanmış sistemler değildir. Bu nedenle böyle sistemlere Newton’ın ikinci yasasını doğrudan uygulayamayız. Böyle durumlarda F = dp/dt eşitliğinin dikkatsizce kullanılması yanlış sonuçlar verecektir. Buna rağmen, momentumun korunumunu tüm sisteme uyguladığımızda (örneğin roket ve yakıtı) elde ettiğimiz sonuçlar kesinlikle doğru olacaktır.
Son cümlede kullanılan tüm sistem ifadesi genişletilmiş, sabit kütleli ve tüm parçacıkları belirli bir sisteme karşılık gelir. Bu durum, F = dp/dt ifadesinin sadece sabit kütleli sistemler için doğru olduğu anlamına gelir. Buna rağmen yasa F = ma şeklinde ifade edildiğinde, bileşke kuvvet sisteme giren veya çıkan kütlenin ikisini de içerecek şekilde alındığında, kütlenin değişimine aldırmaksızın herhangi bir parçacığın veya sistemin hareketini doğrulukla açıklar.
Newton’un üçüncü yasası: Etki-tepki yasası
| “ | Lex III: Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi. | „ |
| “ | Yasa III: Her kuvvete karşılık, her zaman eşit ve ters bir tepki kuvveti vardır: veya iki cismin birbirine uyguladığı kuvvetler her zaman eşit ve zıt yönelimlidirler. | „ |

Daha doğrudan bir çeviri şu şekilde yapılabilir:
| “ | YASA III: Her etki için ona eşit ve zıt yönlü bir tepki vardır: veya iki cismin birbirine uyguladıkları karşılıklı etkiler eşit ve karşıt taraflara yönelimlidirler. — Karşı tarafı iten veya çeken her ne ise, aynı ölçüde karşı taraf tarafından itilir veya çekilir. Eğer parmağınızla bir taşı itiyorsanız, aynı zamanda parmağınız da taş tarafından itilecektir. Eğer bir at, ip ile bağlanmış bir taşı çekiyorsa, at da eşit olarak taş tarafından geriye doğru çekilecektir: gerilmiş haldeki ip gevşemek için, taşı ata çektiği ölçüde, atı da taşa doğru çekecektir ve birinin ilerlemesini engellediği kadar diğerinin ilerlemesini de engelleyecektir. Eğer bir cisim diğerine çarparsa ve uyguladığı kuvvet diğerinin hareketini değiştirse, kendi hareketi de (ortak baskının eşitliği nedeniyle) aynı miktarda ve karşıt yönde bir değişime uğrayacaktır. Eğer cisimler başka engeller tarafından engellenmiyorsa, bu etkiler tarafından oluşturulan değişimler eşittir, ancak bu eşit miktarda değişen bu nicelikler cisimlerin hızları değil, hareketleridir. Hareketler eşit miktarda değiştiğinden, cisimlerin ters taraflara doğru meydana gelen hız değişimleri birbirleri ile ters orantılıdır. Bu yasa sonraki notlarda ispatlanacağı üzere çekim etkilerinde de yer alır. | „ |
Alışılmış olduğu üzere Newton yukarıdaki çeviride momentumdan hareket olarak bahsetmiş, “hız” ile “hareket” arasındaki farka dikkat çekmiştir.
Newton’ın üçüncü yasası, tüm kuvvetlerin etkileşimler olduğunu söyler -yani tek yönlü kuvvet diye bir şey yoktur. Eğer bir A cismi, bir B cismi üzerine bir kuvvet uyguluyorsa B cismi de aynı anda A üzerine aynı büyüklükte bir kuvvet uygular; öyle ki uygulanan bu kuvvetler aynı doğru üzerinde yer alır. Şekilden görüleceği üzere, patenciler birbirlerine büyüklükleri aynı fakat yönleri ters olan kuvvetler uygular. Uygulanan kuvvetler eşit olmasına rağmen ivmelenmeler eşit değildir: Newton’ın ikinci yasasına göre daha zayıf olan patenci daha büyük bir ivme kazanacaktır. Burada dikkat edilmesi gereken konu etki/tepki çiftinin farklı nesneler üzerine etkidiği ve birbirini yok etmediğidir. Newton’ın üçüncü yasasındaki iki kuvvet aynı tiptedir, örneğin, eğer yol, ivmelenen bir araba lastiği üzerinde ileri yönlü bir sürtünme kuvveti uyguluyorsa (ki bu kuvvet, arabanın hareket etmesini sağlayan kuvvettir), bu sürtünme kuvveti Newton’ın üçüncü yasasına göre aynı zamanda lastikleri yol üzerinde geri iter.
Newton üçüncü yasayı, momentumun korunumu yasasını türetmek için kullanmıştır; buna rağmen daha derin bir bakış açısı ile momentumun korunumu, daha temel bir fikirdir (Galileo) dönüşümlerinden Noether teoremi aracılığıyla ispatlanır) ve Newton’ın üçüncü yasasının geçerli olmadığı durumlarda da geçerliliğini korur (örneğin parçacıkların momentum taşıdığı gibi kuvvet alanlarının da momentum taşıması durumunda veya kuantum mekaniğinde).
Önemi ve geçerlilik erimi
Newton yasaları 200 yıldır çeşitli deneyler ve gözlemler ile doğrulanmıştır ve gündelik yaşantımızdaki hızlar ve ölçekler için mükemmel birer yaklaşımdırlar. Newton’un hareket yasaları, yine onun bulduğu evrensel kütleçekim yasası ve kalkülüsün matematiksel yöntemleri ile birlikte, ilk kez geniş çaptaki fiziksel olaylar için niceliksel bir açıklama sağlamıştır.
Bu üç yasa, gündelik koşullarda makroskopik cisimlerin hareketi için iyi bir yaklaşıklık ile geçerlidirler. Buna rağmen, çok küçük ölçeklerde, çok yüksek hızlarda veya çok güçlü kütleçekimsel alanların varlığında geçerliliklerini yitirirler. Bu nedenle yasalar, bir yarı iletkendeki elektrik iletimi, maddelerin optik özellikleri, relavite hesaba katılmadan düzenlenen GPS sistemlerindeki hatalar ve süper iletkenlik gibi olayları açıklamakta kullanılamazlar. Bu tip olayların açıklanabilmesi, Genel Görelilik ve Relativistik Kuantum Mekaniği gibi daha karmaşık fiziksel teorileri gerektirir.
Kuantum mekaniğinde kuvvet, momentum veya konum gibi kavramlar, bir kuantum durumu üzerine işlem yapan, doğrusal operatörler ile tanımlanır. Işığın hızından çok düşük olan hızlarda, bu operatörler Newton yasalarına indirgenir. Işık hızına yaklaşık hızlarda, bir cisim için kuvvetin o cismin momentumunun zamana göre türevi olduğunu söyleyen ikinci yasa orijinal halini (F = d (p) / dt) korusa da, ikinci yasanın bazı yeni sürümleri (yukarıdaki sabit kütle yaklaşımı gibi) geçerliliklerini koruyamamaktadırlar.
Newton’un beşiği

Newton’un beşiği ya da Newton topları, adını Isaac Newton’dan alan, momentumun korunumu yasasının incelendiği ve basit sarkaçların yan yana bağlanması ile oluşan çoklu sarkaçtır.
Animasyonlu resimde de göründüğü üzere, tipik bir Newton’un beşiği, basit bir fizik kanununa göre çalışmaktadır. Toplar, tek bir çizgide hareket ederler. Aynı hizada ve bir sarkaçta yer alan birkaç toptan meydana gelen beşikte, bir top kaldırıldığında topa bir enerji yüklenir. Kaldırılan top, diğer topa değeceği sırada bu enerji, kinetik enerjiye dönüşür. Birinci top, ikinci topa değdiğinde momentumu bu topa aktarır. Bu şekilde en son topa kadar aktarım sürer. Son top aldığı momentum transferi sonucu havaya kalkar ve aynı şekilde oluşan momentum transferi, bu defa sondan başlayarak ilk topa doğru gider.
Hareketi
Eğer bir bilye çekilip bırakılırsa düşer ve diğer bilyelere vurduğunda tamamen durur. Dizinin zıt yönündeki son bilye ise ilk çarpan topun hızını alır ve ilk topun izleyeceği şekilde bir kavisle sallanır. Ortadaki bilyeler sabit kalır, hatta ortadaki toplar sabitlense bile beşik çalışmaya devam eder. Bu da sezgilere aykırıdır çünkü hareket etmeksizin hareket iletilmiş olur. İlk defa gözlemleyen bir kişi bunu görsel olarak ilgi çekici ve sezgilere aykırı bulabilir. Eğer birisi bir insan kuyruğunun sonundan ileriye doğru ittirirse, sondaki insanın kinetik enerjiye maruz kalması yerine bütün insanların ileriye hareketleneceğini düşünür. Aslında meydana gelen şey, ilk darbeden oluşan şokun diğer bilyelerin içinden yayılmasıdır. Otobüs kuyruğundaki insanların aksine çelik gibi sert maddeler bu iletimde gayet başarılıdır. Şok dalgası bir vasıtanın içerisinde ses hızıyla hareket eder. Sesin çelik içindeki hızı (ortalama 4699 m/s) havadaki hızından daha yüksektir. İnsan algısı için birkaç santimetre hareket etme süresi çok küçüktür, benzer bir durum şok dalgası bilyelerin içinden geçerken bilyelerde meydana gelen fiziksel bozulmalarda da gözlemlenebilir. Gerçek dünyada bu işlemlerin hiçbiri mükemmel verimlilikte değildir. Kuvvet; asılı tellerde, havanın sürtünmesinde ve ses oluşumunda kayıplar verir. Sonuncusu apaçıktır ve bilyelerin çıtlama sesleri işitilir. Salınımın sonlarına doğru ortadaki toplar bile basit bir miktar hareket sergiler.
Bir diğer ayrıntı ise, aynı anda birden fazla bilyeyi hareket ettirmektir. İki bilye ile zıt yönde tam iki bilye sıçrar ve geri gelir. Gözle görülür şekilde simetrik olmasına karşın, zıt yöndeki tek bir bilyenin 2 kat daha hızlı gitmemesinin sebebi momentumun ve enerjinin aynı anda korunumudur.
Newton’un evrensel kütleçekim yasası

Newton’un evrensel çekim yasası (klâsik mekaniğin bir parçasıdır) aşağıdaki gibi ifade edilir;
Her bir noktasal kütle diğer noktasal kütleyi, ikisini birleştiren bir çizgi doğrultusundaki bir kuvvet ile çeker. Bu kuvvet bu iki kütlenin çarpımıyla doğru orantılı, aralarındaki mesafenin karesi ile ters orantılıdır:
- F=Gm1m2r2
Burada:
- F iki kütle arasındaki çekim kuvvetinin büyüklüğü,
- G Evrensel çekim sabiti 6.67 × 10-11 N m2 kg-2 ,
- m1 birinci kütlenin büyüklüğü,
- m2 ikinci kütlenin büyüklüğü,
- r ise iki kütle arasındaki mesafedir.
SI birimlerinde, F Newton (N), m1 ve m2 kilogram(kg), r Metre (m) dir ve G sabiti yaklaşık olarak 6.67×10−11 N m2 kg−2’a eşittir. G ilk kez İngiliz bilim insanı Henry Cavendish tarafından, “Philosophiae Naturalis Principia Mathematica”nın basımından 111 ve Newton’un ölümünden 71 yıl sonra ölçülmüştür; bu yüzden Newton’un hesaplamalarının hiçbirinde “G” sabiti kullanılmamış, bunun yerine bir kuvvete bağıl başka bir kuvvet hesaplamıştır.
Newton’un çekim yasası Coulomb yasası’na benzer. Newton’un yasası iki kütle arasındaki çekim kuvvetini hesaplamak için kullanılırken, benzer şekilde, Coulomb yasası yüklü iki iletkenin arasındaki elektriksel kuvvetin büyüklüğünü hesaplamak için kullanılır. Coulomb yasası’nun denkleminde Newton’un denklemindeki kütlelerin yerine yüklerin çarpımını içerir. Böylece Coulomb yasası’na göre elektriksel kuvvet yüklerin çarpımının aralarındaki mesafeye bölümüyle doğru orantılıdır.
Yerçekimi ivmesi
a1‘e birinci kütleye etkiyen yerçekimi ivmesi diyelim. Newton’un ikinci yasasına göre F = m1 a1, a1 = F / m1‘dır. Fi önceki denklemden yerine koyarsak:
- a1=Gm2r2 olur.
Aynı şekilde a2‘de buna benzerdir.
SI birimlerinde, yerçekimi ivmesi (veya genel olarak ivme), metrenin saniyenin karesine oranıdır (m/s2 or m s−2). SI olmayan birimlerde ise birimi Galileo (Gal), g-kuvveti (İng. İngilizce: g-force), ayak bölü saniyenin karesidir.
Bir kütleyi Dünya’ya çeken kuvvet, aynı zamanda Dünya’yı da kütleye doğru çeker. Bunların ivmeleri ise aşağıdaki gibi hesaplanır:
- a1+a2=Gm1+m2r2
Eğer m1 m2‘ye göre göz ardı edilebilirse, küçük kütleler yaklaşık olarak aynı ivmeye sahip olur. Bununla beraber m1 epeyce büyükse birleşik ivme göz önüne alınmalıdır.
Eğer r bir objenin yörüngesi boyunca oransal olarak çok az değişirse – bir objenin Dünya’nın yüzeyine yakın bir yerde düşmesi gibi – yerçekimi ivmesi sabite oldukça yakın olur. Büyük bir kitle boyunca, “r”deki değişiklikler ve yer çekimi kuvvetindeki ardı ardına değişiklikler gözle görülür bir gel-git kuvveti oluşturabilir. Örneğin, Dünya’nın yakın ve uzak yüzleri ile Ay arasındaki mesafe farkı 6.350 km dir. 385.000 km ortalama mesafeye göre küçük bir fark olsa da bu, Ay’ın Dünya’nın okyanusları üzerinde bir çekim kuvveti oluşturmasını ve böylece gelgit oluşumuna sebep olur.
Uzaysal boyutu olan kütleler
Eğer ilgilenilen kütlelerin uzaysal boyutu varsa (teorik olarak noktasal olmaktan ziyade) o zaman aralarındaki çekim kuvveti, bu kütleleri oluşturan kavramsal noktaların katkılarının toplanmasıyla hesaplanır. Limitte bileşen nokta kütleler sonsuz derecede küçüldükçe, kuvvetin (aşağıda vektör formu görülüyor) iki fiziksel kütlenin boyutlarına oranlarının integrali gerekir.
Bu yolla kütlesi küresel olarak simetrik dağılmış kütle, haricî kütlelere tüm objelerin kütleleri merkezindeki bir nokta etrafında toplanmış gibi aynı çekim etkisini uygular. (Bu, genellikle küresel simetrik olmayan kütleler için geçerli değildir.)
Küresel simetrik dağılımlı bir malzemenin içindeki kütlelerin çekimsel kuvvetini bulmak için Newton’un kabuk teoremi (İng. İngilizce: Shell’s theorem) kullanılabilir. Bu teorem, bize kütle dağılımının farklı parçalarının kütle dağılım merkezinden r0 kadar uzaktaki bir parçayı nasıl etkilediklerini açıklar:
- r < r0 yarıçapında bulunan kütle, r0’da sanki kütlenin tamamı bu yarıçapta bir küredeki tüm kütlenin kütle dağılımı merkezinde toplanmış gibi aynı kuvvete sebep olur (yukarıda yazıldığı gibi).
- r > r0 yarıçapında bulunan kütle r0’ da net çekim kuvveti oluşturmaz. Örneğin, r0 noktasındaki kürenin elementleri tarafından etkilenen münferit kuvvetler birbirlerini götürürler.
Örneğin, bir sonuç olarak, eşit dağılan bir kalınlık ve yoğunluğa sahip olan bir kabuk boyunca net çekim kuvveti sıfırdır.
Vektör formu


Newton’un evrensel çekim yasası, hem çekim kuvvetinin büyüklüğünü hem de doğrultusunu gösteren bir vektör olarak yazılabilir. Bu formülde kalın yazılar vektörleri göstermektedir:
- F12=−Gm1m2|r12|2r^12
Burada
- F12: 1 numaralı cismin 2 numaralıya uyguladığı kuvvet,
- G: çekim sabiti (yerçekimi sabiti olan g ile karıştırılmamalı),
- m1 ve m2 sırasıyla birinci ve ikinci objelerin kütleleri,
- |r12| =|r2−r1| 1 ve 2 objeleri arasındaki mesafe,
- r^12 =def r2−r1|r2−r1| ise 1’inci objeden 2.’ye olan birim vektördür.
Eşitliğin vektörel formunun, F nin artık vektörel bir değer olması ve sağ tarafın uygun birim vektörle çarpılmış olması haricinde, daha önceden verilen skaler formla aynı olduğu görülebilir. Ayrıca buradan şu da görülebilir: F12 = – F21.
Çekim Alanı
Çekim alanı uzayda verilen herhangi bir noktadaki objeye, birim kütle başına uygulanan çekim kuvvetini tanımlayan vektör alanıdır. Aslında bu o noktadaki çekim ivmesine eşittir.
Eğer birden fazla obje varsa(dünya ve ay arasındaki bir roket gibi) kullanışlı hale gelen bir genelleştirmedir. İki obje için(örneğin obje 2 bir roket ve obje 1 de dünya olsun) basitçe r12 yerine r ve m2 yerine m yazabiliriz ve çekim alanınıg(r) aşağıdaki gibi tanımlayabiliriz:
- g(r)=−Gm1|r|2r^
Böylece:
- F(r)=mg(r) olur.
Bu formül alana sebep olan objelerden bağımsızdır. Bu alan ivme birimlerine sahiptir ve bu da SI birimlerinde m/s2‘dir.
Çekim alanları aynı zamanda korunumlu alanlardır, yani, bir pozisyondan öbürüne çekim tarafından yapılan iş yoldan bağımsızdır. Bunun sonucunda potansiyel aşağıdaki gibi potansiyel V(r) alanı oluşur:
- g(r)=−∇V(r).
Eğer m1 noktasal bir kuvvet ise veya homojen dağılmış bir kütle ise, kürenin dışındaki kuvvet alanı g(r) izotropiktir (yönden bağımsızdır), örneğin, sadece kürenin merkezinden olan r mesafesine bağlıdır. Bu durumda;
- V(r)=Gm1r.
Newton’un teorisinin problemleri
Newton’un tanımı birçok pratik amaç için yeterli şekilde doğrudur ve bu yüzden geniş şekilde kullanılır. Boyutsuz değerler φ/c2 ve (v/c)’nin ikisi de küçük olduğunda kullanılabilir, burada φ çekimsel potansiyel, v incelenen objelerin hızı ve c ışık hızıdır. Örnek olarak, Newtonien çekim Dünya/Güneş sisteminin doğru bir tanımını sağlar, çünkü;
- Φc2=GMgunesryorungec2∼10−8,vyerc=2πryorunge(1 yr)c∼10−4
burada rorbit dünyanın güneş etrafındaki yörüngesinin yarıçapıdır.
Boyutsuz değişkenlerden biri büyük olduğu durumlarda, sistemi tanımlamak için genel görelilik kullanılmalıdır. Genel görelilik, küçük potansiyel ve düşük hız sınırlarında Newton’un çekime dönüşür bu yüzden, Newton’un çekim yasası için sıklıkla genel göreliliğin düşük çekim limiti denir.
Teorik kaygılar
- Çekim arabulucusunu hemen bulma gibi bir ihtimal yoktur. Çekimsel kuvvet ile bilinen diğer temel kuvvetler arasındaki ilişkiyi tanımlamak için teorisyenler tarafından yapılan teşebbüsler, 50 yıldır gözle görülür bir ilerleme kaydedilmiş olsa da, henüz sonuca ulaşmamıştır. Newton bile açıklanamaz uzaktan etkileşim konusunda kendini yetersiz hissetmiştir.
- Newton’un teorisi çekimsel kuvvetin ani iletimini gerektirir. Genel göreliliğin geliştirilmesinden önce uzay ve zamanın doğası ile ilgili yapılan klasik varsayımlar, yayılım gecikmesi kararsız yörüngelere sebep olur.
Gözlemle uyuşmazlıklar
- Newton’un teorisi gezegenlerin, özellikle Merkür’ün, yörüngelerinin güneşe en yakın noktalarının(günberi) yalpalamalarını tam olarak açıklamaz. Newton’un tahminlerle, gözlenen yalpalama arasında, diğer gezegenlerin çekimsel sürüklemelerinden kaynaklanan, 43/3600 derecelik(43 arcsecond) bir uyumsuzluk bulunmaktadır.
- Newton’un teorisi kullanılarak tahmin edilen sapma gözlenenin sadece yarısıdır. Genel görelilik ise gözlemlere daha yakındır.
Çekimsel ve ataletsel kütlelerin tüm kütleler için aynı olmasıyla ilgili gözlenen gerçek, Newton’un sisteminde açıklanamamaktadır. Genel görelilik bunu bir varsayım olarak alır.
Newton’un şüpheleri
Newton kendi anıtsal çalışmasında çekim yasasını formüle edebiliyorken, kendi eşitliklerinin öne sürdüğü uzaktan etkileşim(action at a distance) kavramı yüzünden kendini derin şekilde rahatsız hissediyordu. Kendi sözleriyle “ bu gücün sebebini hiçbir zaman tespit edememişti”. Tüm diğer durumlarda, kütleler üzerine etkiyen çeşitli kuvvetlerin sebebini açıklamak için hareket olgusunu kullanmıştır, fakat, çekimle ilgili durumda, çekim kuvvetini üreten hareketi deneysel olarak tanımlayamamıştı. Dahası, yer üzerindeki bu kuvvetin sebebine gelince bir hipotez önermeyi dahi reddediyordu.
“Filozoflar şimdiye kadar çekim kuvvetinin kaynağı için boşuna doğa araştırmasına girişmişlerdir” diye pişman olmuştur, çünkü “birçok sebepten dolayı”, doğa olgusunun temeli olan, “şimdiye kadar bilinmeyen sebepler”in varlığına ikna olmuştur. Bu temel olgular hala araştırılmaktadır ve hipotezler çok olsa da tanımlayıcı yanıt henüz bulunamamıştır. Newton’un 1713 tarihli ve “Principia”nın ikinci baskısı olan “General Scholium”unda:
- “Daha henüz çekimle ilgili bu özelliklerinin sebeplerini olgudan keşfedebilmiş değilim,ve yalandan hipotez uydurmadım…Çekimin varlığı ve açıkladığım yasalara göre işlemesi ve uzaysal kütlelerin(yıldız, gezegen gibi) hesaplamasına yaptığı hizmetler yeterlidir. Bir kütle bir başkasını bir vakum içinde, başka hiçbir şeyin arabuluculuğu olmadan etkiler, etkileri ve kuvvetleri tarafından ve onların içine diğerine taşınabilmesi bence büyük bir garabettir ve bence bu yüzden, felsefi malzemelerde düşünmenin bileşen yetisine sahip hiç kimse, onun içine düşmez.”
- 1751 – Frederick, Galler Prensi, İngiliz tahtının varisi (d. 1707)
- 1763 – Marco Foscarini, Venedik Cumhuriyeti’nin 117’nci dükü (d. 1696)
- 1837 – John Constable, İngiliz ressam (d. 1776)
- 1850 – John C. Calhoun, Amerikalı devlet adamı (d. 1782)
- 1855 – Charlotte Brontë, İngiliz romancı (Jane Eyre adlı yapıtıyla ünlü) (d. 1816)
- 1869 – Allan Kardec, Fransız yazar ve Deneysel Spiritüalizmin kurucusu (d. 1804)
- 1870 – Thomas Cooke, Kanadalı Katolik rahip ve misyoner (d. 1792)
- 1898 – Eleanor Marx, Marksist yazar ve politik eylemci (d. 1855)
- 1907 – Léo Taxil, Fransız gazeteci ve yazar (d. 1854)
- 1910 – Jean Moréas, Yunan asıllı Fransız şair (d. 1856)
- 1917 – Emil Adolf von Behring, Alman hekim ve Nobel Tıp veya Fizyoloji Ödülü sahibi (d. 1854)
- 1943 – Pavel Milyukov, Rus tarihçi ve liberal politikacı (d. 1859)
- 1945 – Anne Frank, Yahudi yazar (yazdığı günlüklerle ünlü, Yahudi Soykırımının simge isimlerinden) (d. 1929)
- 1945 – Hans Fischer, Alman kimyager (d. 1881)
- 1970 – Semyon Timoşenko, Sovyet komutan (d. 1895)
- 1975 – Munis Faik Ozansoy, Türk şair ve yazar (d. 1911)
- 1976 – Paul Strand, Amerikalı fotoğraf sanatçısı (d. 1890)
- 1980 – Jesse Owens, Amerikalı atlet (d. 1913)
- 1981 – Enid Bagnold, İngiliz yazar (d. 1889)
- 1993 – Brandon Lee, Çin kökenli Amerikalı aktör (d. 1965)
- 1995 – Selena, Amerikalı şarkıcı ve söz yazarı (d. 1971)
- 2001 – Clifford Shull, Amerikalı fizikçi ve Nobel Fizik Ödülü sahibi (d. 1915)
- 2008 – Jules Dassin, Amerikalı sinema yönetmeni (d. 1911)
- 2008 – Pippa Bacca, İtalyan sanatçı ve aktivist (d. 1974)
- 2009 – Atilla Konuk, Türk siyasetçi ve sporcu (d. 1923)
- 2009 – Aydın Babaoğlu, Türk sinema oyuncusu (d. 1953)
- 2009 – Raúl Alfonsín, Arjantinli avukat ve siyasetçi (d. 1927)
- 2010 – Ana Novac, Rumen yazar (d. 1929)
- 2010 – Alp Can, Türk gazeteci (d. 1961)
- 2012 – Dale R. Corson, Amerikalı fizikçi ve akademisyen (d. 1914)
- 2013 – Yaşar Güner, Türk tiyatro, sinema ve dizi oyuncusu (d. 1943)
- 2015 – Mehmet Selim Kiraz, Türk savcı (d. 1969)
- 2016 – Ronnie Corbett, İskoçyalı oyuncu ve komedyen (d. 1930)
- 2016 – Georges Cottier, İsviçreli kardinal (d. 1922)
- 2016 – Hans-Dietrich Genscher, Alman politikacı (d. 1927)
- 2016 – Zaha Hadid, İngiliz mimar (d. 1950)
- 2016 – Imre Kertész, Macar yazar ve Nobel Edebiyat Ödülü sahibi (d. 1929)
- 2016 – Denise Robertson, İngiliz program sunucusu (d. 1932)
- 2017 – Halit Akçatepe, Türk tiyatro, sinema ve dizi oyuncusu (d. 1938)
- 2017 – Gilbert Baker, Amerikalı LGBT hakları aktivisti ve bayrak tasarımcısı (d. 1951)
- 2017 – William Thaddeus Coleman, Jr., Amerikalı avukat ve siyasetçi (d. 1920)
- 2017 – Mike Hall, Britanyalı bisiklet yarışçısı ve organizatörü (d. 1981)
- 2017 – Radley Metzger, Amerikalı pornografik film yapımcısı (d. 1929)
- 2017 – Roland W. Schmitt, Amerikalı iş uzmanı fizikçi (d. 1923)
- 2018 – Frank Aendenboom, Belçikalı oyuncu (d. 1941)
- 2018 – Margarita Carrera, Guatemalalı yazar, akademisyen ve filozof (d. 1929)
- 2018 – Luigi De Filippo, İtalyan oyuncu, tiyatro yönetmeni ve oyun yazarı (d. 1930)
- 2018 – Mükerrem Kemertaş, Türk ses sanatçısı (d. 1938)
- 2019 – Peter Coleman, Avustralyalı yazar, gazeteci ve siyasetçi (d. 1928)
- 2019 – Cesare Dujany, İtalyan siyasetçi (d. 1920)
- 2019 – Ralph S. Greco, Amerikalı cerrah ve heykeltıraş (d. 1942)
- 2019 – Nipsey Hussle, Amerikalı Hip-Hop sanatçısı (d. 1985)
- 2019 – Eva Moser, Avusturyalı satranç oyuncusu (d. 1982)
- 2019 – Yves Préfontaine, Québec doğumlu Kanadalı şair ve yazar (d. 1937)
- 2019 – Hedi Türki, Tunuslu sanatçı ve eğitimci (d. 1922)
- 2020 – Mark Azbel, Sovyet-İsrailli fizikçi (d. 1932)
- 2020 – Jim Bailey, Avustralyalı orta mesafe koşucusu (d. 1929)
- 2020 – Julie Bennett, Amerikalı aktris ve seslendirme sanatçısı (d. 1932)
- 2020 – Cristina, Amerikalı şarkıcı (d. 1959)
- 2020 – Viktar Daşkeviç, Beyaz Rus aktör (d. 1945)
- 2020 – Pape Diouf, Senegalli eski gazeteci ve spor yöneticisi (d. 1951)
- 2020 – Rafael Gómez Nieto, İspanyol asker (d. 1921)
- 2020 – James Stuart Gordon, Strathblane Baronu Gordon, İskoç iş insanı, siyasetçi ve yönetici (d. 1936)
- 2020 – Andrew Jack, İngiliz dublaj sanatçısı, eğitimci ve aktör (d. 1944)
- 2020 – Abdülhalim Haddam, Suriyeli siyasetçi (d. 1932)
- 2020 – Eva Krížiková, Slovak aktris (d. 1934)
- 2020 – Vincent Marzello, Amerikalı aktör (d. 1951)
- 2020 – Gita Ramjee, Ugandalı-Güney Afrikalı bilim insanı ve araştırmacı hekim (d. 1956)
- 2020 – Wallace Roney, Amerikalı caz trompetçisi (d. 1960)
- 2020 – Kiyoshi Sasabe, Japon film yönetmeni (d. 1958)
- 2020 – Peter J. N. Sinclair, İngiliz ekonomist ve profesör (d. 1946)
- 2020 – Michael Wakelam, Britanyalı moleküler biyolog, profesör (d. 1955)
- 2021 – Anzor Erkomaishvili, Gürcü şarkıcı, besteci, halk müziği araştırmacısı ve siyasetçi (d. 1940)
- 2021 – Kemal Ganzuri, Mısırlı bir politikacı (d. 1933)
- 2021 – Cleve Hall, Amerikalı özel efekt sanatçısı, makyöz ve aktör (d. 1959)
- 2021 – Jadwiga Wysoczanská, Çek opera sanatçısı (d. 1927)
- 2021 – Carlos Pedro Zilli, Brezilya doğumlu Gine-Bissauan Roma Katolik Kilise’sinin piskoposu (d. 1954)
- 2022 – Georgi Atanasov, Bulgar siyasetçi (d. 1933)
- 2022 – Rıdvan Bolatlı, Türk eski millî futbolcudur (d. 1928)
Tatiller ve özel günler
- Azerbaycanlıların Soykırım Günü

 Osmanlı Gazetesi Medya İmparatorluğu
Osmanlı Gazetesi Medya İmparatorluğu












































